Topics in Computer Mathematics - Number Systems
Although computer designers can arbitrarily choose the
size of the register to be used as
well as the size of the fields, most modern systems follow the standards
established by
the IEEE (Institute of Electrical and Electronic Engineers). This standard
provides two
formats, a single precision format and a double precision format. They are
summarized
in table TN4. When all of the bits in the format are 0's, the number is assumed
to be
zero.
| Feature | Single Precision Format | Double Precision Format |
| Register Length | 32 bits | 64 bits |
| Mantissa | 23 + 1 implied | 52 + 1 implied |
| Exponent, Bias | 8 bits, 127 | 11 bits, 1023 |
Table. TN4. IEEE Floating Point Standard
Conversion of Decimal numbers to Binary Floating Point
The following steps are required in order to convert a decimal number to its
binary
floating point representation.
a. Convert the decimal number to a binary number (This includes either
expanding 10x into decimal form , if x is small, or converting it to
2y)
b. Put the binary number into floating-point form
c. Normalize the binary number
d. Convert the exponent to binary, and add the bias
e. Specify the sign as a binary digit
In the following examples, we’ll assume a floating point format with a 16 bit
register to
hold the FP number, having
1 sign bit
4 exponent bits, with a bias of 7
11 mantissa bits, plus 1 implied bit
Note that the exponent range in this format is -7 through +8. This means that
the
smallest (absolute value) number representable is
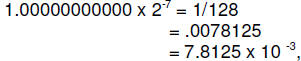
and the largest is
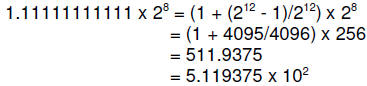
Example 27. Convert 54.23 to the above binary format.
a.
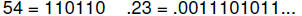 (11101011 repeats)
(11101011 repeats)
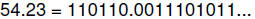
b. and c.
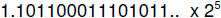 (note that 15 fraction bits are shown;
(note that 15 fraction bits are shown;
only 11 of them will be retained in the specified format.)
d. 5 = 0101; add the bias of 7: 0101 +111 = 1100.
e. Sign = 0
In floating point hardware format,
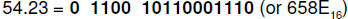 Notice that
Notice that
the 1 to the left of the binary point is not included.
Example 28. Convert
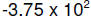 to binary FP format
to binary FP format
a. The easy way to do this is to write the number in integer format (375) and
convert it to binary. In practice, however, the exponents are likely to be quite
large and it would not be feasible to take this approach. Let’s develop a
general
rule for converting 10x to 2y.
We want 10x = 2y; that is, we want to solve this equation
for y in terms of x. Take
the log to the base 2 of both sides
Thus, any exponent of 10 can be converted to an exponent
of 2 by multiplying the
decimal exponent by
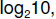 , which is roughly equal to 3.322... So, for
this
, which is roughly equal to 3.322... So, for
this
example, we could say
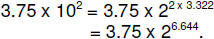
Since we don’t allow for fractional exponents, we will
have to make the following
adjustment:
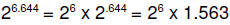 (using a calculator)
(using a calculator)
and
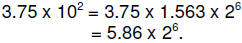
Converting 5.86 to binary gives us
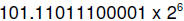
[Note that when converting a fraction from decimal to binary we can stop
multiplying by two when we have generated enough digits (counting both the
integer and fraction portions of the number) to fill the mantissa field of the
FLP
format.]
b. and c.
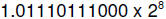
d. 4. Exponent 8 biased by 7 is 15 = 1111.
e. Sign (-) is 1.
The final result is
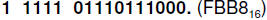
Note that by converting 102 to 2y, we introduced several
rounding and truncation
errors. Compare the result above with what we get by simply converting 375:
a. 375 = 101110111
b. and c.
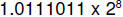
d. Exponent is still 8 --> 1111 in biased form
e. Sign = 1
The final result is
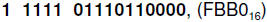 which differs from our previous
which differs from our previous
result only in the eighth fractional position, so we are off by 2-8
or 1/256 = .0039.
Convert binary floating point numbers to Decimal numbers
The procedure is
a. Convert the exponent to decimal and subtract the bias
b. Evaluate 2x if possible (x is small) or convert to 10y
c. Convert the mantissa to decimal and add 1 (to restore the implied digit)
d. Combine the sign and the results of steps 1 through 3 into the decimal
form of the number
Example 29. Convert
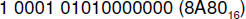 to a decimal number.
to a decimal number.
a. The exponent is
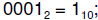 subtracting the bias (7) gives -6.
subtracting the bias (7) gives -6.
b.
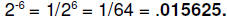 Alternatively,
Alternatively,
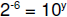 ; taking the
; taking the
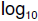 of both
of both
sides gives
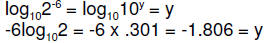
[That is, just as an exponent of 10 can be converted to an
exponent of 2 by
multiplying by
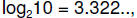 we can convert an exponent of 2 back to an
we can convert an exponent of 2 back to an
exponent of 10 by multiplying by
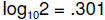 .]
.]
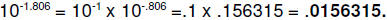 Compare this with .015625; we
Compare this with .015625; we
will continue with the latter, since it contains no rounding or truncation
errors.
c. .0101 = 5/16 = .3125; restoring the implied one = 1.3125
d.
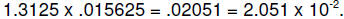 (Either form is acceptable)
(Either form is acceptable)
The concepts involved in the last two examples are important, whereas the actual
numerical manipulations are merely tedious. The following practice problems
represent
the kinds of questions one might actually be asked to answer on an exam or in
real life.
| Practice Problems - Binary Floating Point Numbers 1. Using the floating point register format given above for the examples, show the register contents for the following binary floating point numbers:
2. What is the minimum number of exponent bits
required to accommodate the
3. What is the binary floating point number (in
the form b.bbb... x 29) represented
5. The following hex number represents the
contents of an IEEE floating point |





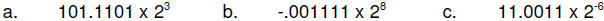
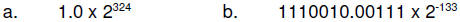
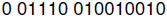 (five bit exponent, bias = 15)
(five bit exponent, bias = 15)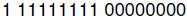 (eight bit exponent, bias = 127)
(eight bit exponent, bias = 127)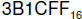 (six bit exponent, bias = 31)
(six bit exponent, bias = 31)