Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

MATH 430 Chapter 1 Exercise 6

Prove that the fourth root of 2 is irrational.

To prove that the fourth root of 2 is irrational, we can prove that all (integer) roots of 2 are
irrational.

Suppose there is a rational root. Any rational number can be written as a/b, where a and b are
whole numbers, and “a and b have no more common factors”.

If that's true, then the nth root of 2 = a/b. So 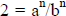, which implies, 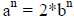. Now if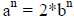
, it follows that an is 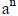even number (since 2 time anything is always even, if the "anything"
is a whole number).

Notice that if 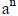is even, then a must be even. If a were odd, then no matter how many times you
multiplied it by itself you'd always end up with an odd number.
If a is an even number, we could write it as 2k (k can be anything - the point is, 2*k must be
even, so writing a like this shows that it is even).

So we have . Divide both sides by 2:

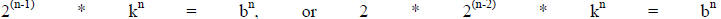
Which shows that 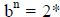(something), so 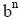is even. Recall from earlier, if 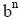is even, then b
must be even.

We have just shown that a and b are both even. But that goes against the earlier statment that a
and b had no common factors. So we've ended up proving that a/b have no common factors, and
also that they do have a common factor, which is impossible.

Since the other assumption was "the nth root of 2 is rational", that's another way of saying "it's
impossible that the nth root of 2 is rational" or "the nth root of 2 is always irrational"

QED

Home