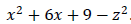Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Factoring Trinomials

Special Product Formulas

Recall:

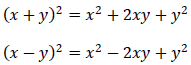
*Notice: Perfect squares on both ends of the trinomial!

Example: Factor: .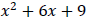

Example: Factor:.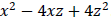

Since the product of two binomials is often a trinomial, we expect that many trinomials will factor as two binomials.

But not all…

Test for Factorability

A trinomial of the form 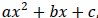with integer coefficients and a ≠0, will factor into two binomials with integer coefficients if the value of 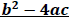is a perfect square. If 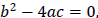, the factors will be the same.

Example 4: Test for factorability:

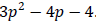
Example 5: Test for factorability:

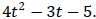
The AC Method

Example 1: Factor: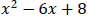

Always first test for factorability:

For each factorable trinomial of the form 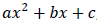, multiply the factors a and c. Then list all possible factorizations of ac.

Choose the factorization where the sum of the factors is b. Then rewrite the trinomial using the chosen factors instead of b.

Factor by grouping.

Example 2: Factor: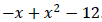

Begin by writing the polynomial in the form 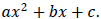. Then test for factorability:

ac:

Example 3: Factor: .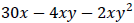

When possible we will always want to factor out a common factor before using the ac method and before testing for factorability.

Example 6: Factor: .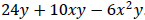

Example 7: Factor: .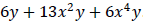

Using Substitution to Factor Trinomials

Example 9: Factor: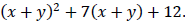

Factoring by Grouping

Example 10: Factor:

Home