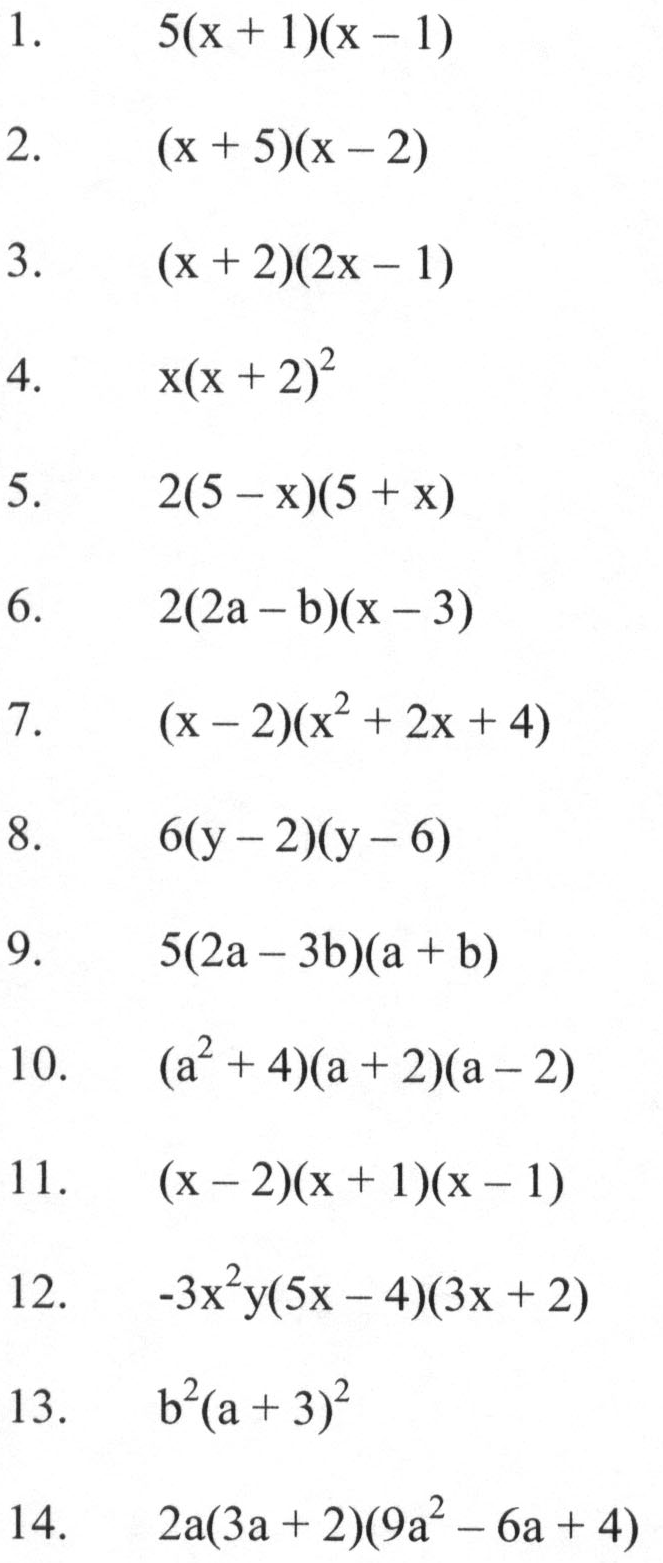Factoring Polynomials

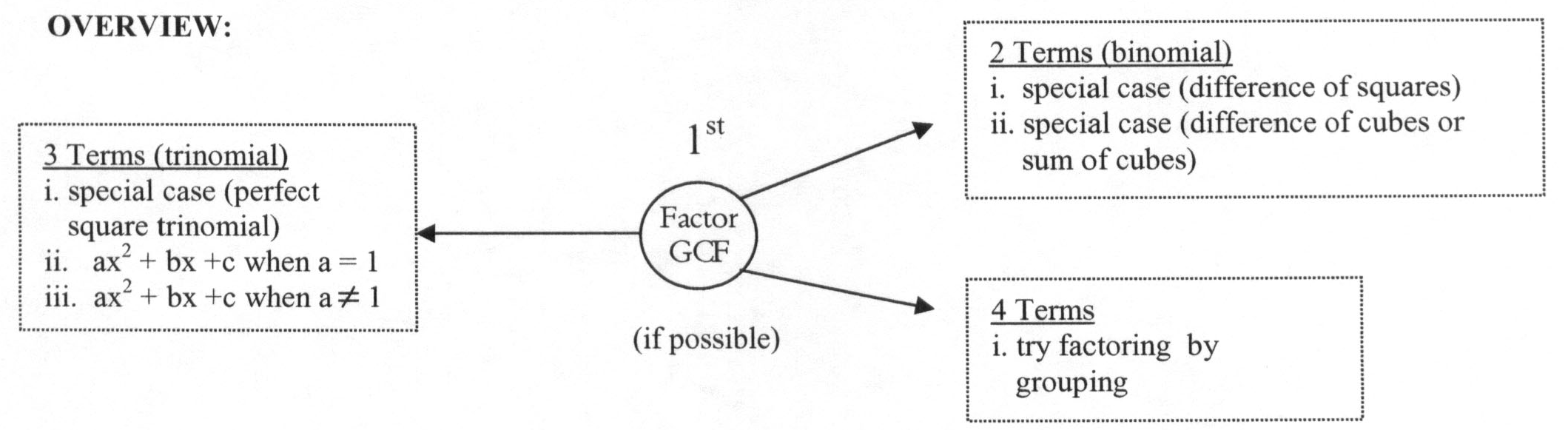
When factoring is completed:
1) Check to see if one of the polynomial factors can be factored again.
2) Double check for other GCFs (greatest common factors)

I.GCF Greatest Common Factor

> A factor that every term in the expression has in common
> Reverse distribution

Examplea: To find the GCF for 12x⁴ - 6x³+ 3x²

12x⁴-6x³+3x² means (2·2·3·x·x·x·x)-(2·3·x·x·x)+(3·x·x)

all three terms have 3 and x·x as common factors

So the GCG is 3x²

Note:
1) 3 is the greatest common numerical factor because it is the largest number that divides into every term evenly.
2) x² is the greatest common variable factor because it is the variable to the largest power that divides evenly into all three terms.

To factor 12x⁴-6x³+3x² thi9ne reverse distribution 3x²(4x²-2x+1)

II. Factoring Trinomials (ax²+bx+c)

i) Special Case (Perfect Square Trinomial)
Strategy: Test the trinomial to see if it satisfies the conditions of a Perfect Square Trinomial.

A Perfect Square Trinomial:
A²+2AB+B² factors into (A+B)(A+B) which can be written (A+B)² or
A²-2AB+B² factors into (A-B)(A-B) which can be written (A-B)²

TEST:i) 1^st and last terms must be perfect squares.
ii)│middle term │must equal 2 times the roots of the 1^st and last terms.

Example: Factor 9x²-24x+6

Test:
i) 1^st term is 9x² (3x²) and last term is 16 (4)², both perfect squares with roots 3x and 4 as shown.
ii) does the│ middle term│ 24x equal 2(3x)(4)? YES!

The trinomial passes both test. It is a Perfect Square Triniomial of the type
A²-2AB+B²=(A-B)² where 3x →A and 4 →B

Solution:(3x-4)²

ii) For a = 1 (lead coefficient is 1)

Strategy: Find the product ac then determine which factor pairs of ac add up to b.

Ecample: Factor x²-x-12 Note: a=1,b=-1,and c=-12

ac==>(1)(-12)=-12=ac

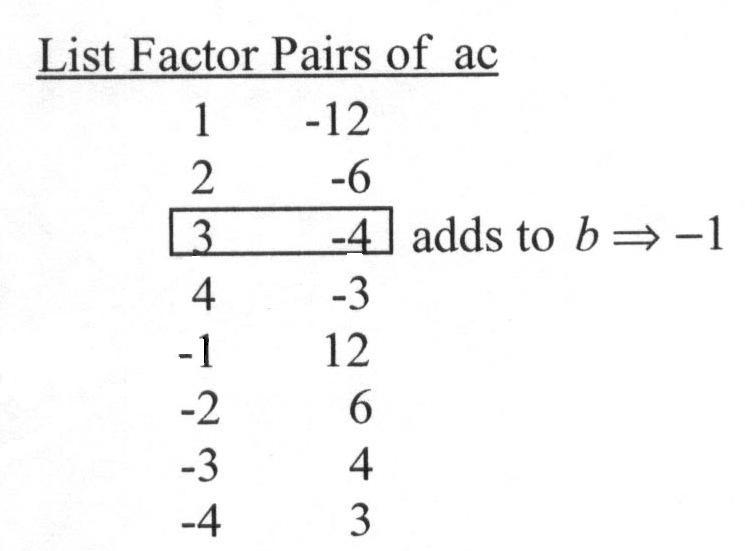
Note:
i) You don’t have to list all factor pairs, just find the two that add to b.
ii) If there are no factor pairs that add to b then the polynomial is "prime".

Solution must be of the form (x _)(x _) where the factor pair and corresponding positive or negative sign supply the missing terms.

Solution:(x+3)(x-4)

iii) For a≠1

Strategy: Find the product ac then determine the factor pairs of ac that add up to b.

Examole: Factor 4x²-25x-21 Note: a=4.b=-25,c=-21

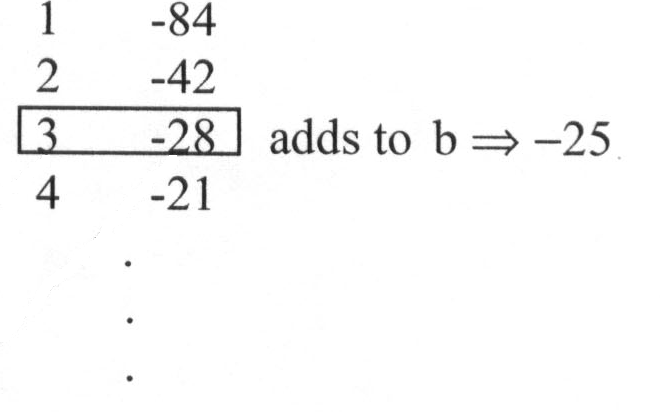
Note:  i)  You don't have to list all factor pairs, just find the two shat add to b.

    ii) If there are no factor pairs that add to b then the polynomial is " prime".

Solution must be of the form (_x  _)(_x  _)

Clues to help you find the missing coefficients and terms:

i) List the factor pairs of a to find possible coefficients of x.
ii) List the factor pairs of c to possible missing final terms.

iii)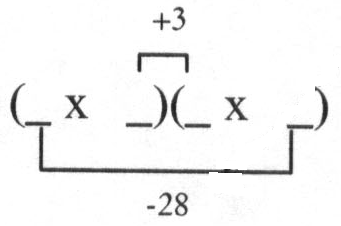Product of "inners" and "outers" must be from the list of factor pairs of ac above that  to b.

Solution:(4x+3)(x-7)

III. Factor by Grouping(4 Terms)

Strategy: Group the four terms in pairs and find the GCF of each pair. Both pairs should then have

a common binomial factor.

Example 1:Factor 3ax-3ay-2bx+2by

3ax-3ay-2bx+2by

GCF of 1^st group is 3a
GCF of 2^nd group is -2b

(Note: If the two groups are separated by a subtraction always factor out a negative GCF from the

second group.)

Factoring each group yields  3a(x-y)-2b(x-y)

Both have a common binomial factor (x-y) which can be factored out leaving the other factor(3a-2b).

Solution:   (x-y)(3a-2b)

Example 2:  Factor 4X²-25X-21

Strategy: Notice!...this polynomial is the same as in section II and it doesn't have 4 terms. But,

if we replace the middle term-25x with the factor pair of ac from the list that adds to -25 we can

write this trinomial with 4 terms and solve by grouping .This is an alternative way of factoring a

trinomial where a≠1.

4x²-28x+3x-21
GCF of 1^st group is 4x
GCF of 2^nd group if 3

Factoring each group yields 4x(x-7)+3(x-7)

Both have a common binomial factou (x-7) which can be factored out leaving the other factor(4x-3)

Solution: (x-7)(4x-3)

Ⅳ. Special Cases (2 Terms)

  i) Difference of Squares

Strategy: Check the binomial to see if it is a difference of squares.

A Difference of Squares A²-B² factors into (A+B)(A-B)

TEST:
i) 1^st and last terms must be perfect squares.
ii) Must be a subtraction.

NOTE: Besides a possible common factor, the Sum of Squares A² + B² is PRIME (not factorable).

Example: Factor 9x²-16

Test:
i) 1^st term is 9x² →(3x)² and last term, is 16→ (4)²,both perfect squares with roots 3x and 4 as shown.
ii) are we subtracting? YES!

The binomial passes both test. It is a Difference of Squares of the form
A²-B² = (A+B)(A-B) where 3x →A and 4→ B

Solution: (3x+4)(3x-4)

ii) Difference OR Sum of Cubes

Strategy: Check the binomial to see if it is a difference of cubes or a sum of cubes.

A Difference of Cubes A3-B3 factors into (A-B)(A²+AB+B²)
A Sum of Cubes A3+B3 factor into (A+B)(A²-AB+B²)

Note: The trinomial factor is often PRLME and cannot be factored further.

TEST:
i) 1^st and last terms must be perfect cubes.
ii) Can be erther a subtraction OR an addition.

Example 1: Factor 27x³+8

Test:
i) 1^st term is 27x³ →(3x)³ and last term is 8→ (2)³,both perfect cubes with roots 3x and 2 as shown.
ii) it is the sum of cubes.

The binomial is a Sum of Cubes of the form A³+B³ = (A+B)(A²-AB+B²)
where 3x→ A and 2 →B

Solution: (3x+2)(9z²-6x+4)

Example 2: Factor 1-64x³

Test:
i) 1^st term is 1 →(1)³ and last term is 64x³ →(4x)³, both perfect cubes with roots 1 and 4x as shown.
ii) it is the difference of cubes.

The binomial is a Difference of Cubes of the form A³-B³ = (A-B)(A²+AB+B²)
where 1 →A and 4x→ B

Solution: (1-4x)(1+4x+16x²)

WORKED EXAMPLES

1. Factor 16x⁴-1

(4x²)²-(1)² Difference of Squares
(4x²+1)(4x²-1) Another Difference of Squares!
(4x²+1)((2x)²-(1)²)
(4x²+1)(2x+1)(2x-1)

2. Factor 3x²+27

3(x²+9)
GCF
(X²+9) can NOT be factored further it is the Sum of Squares which is prime.

3. Factor 8a³+27b³

(2a)³+(3b)³ Sum of Cubes
(2a+3b)(4a²-6ab+9b²)

4. Factor 2x²-xy-6y²

(_x_y)(_x_y) Factor pairs of ac = -12 that add to the middle are 3 and -4

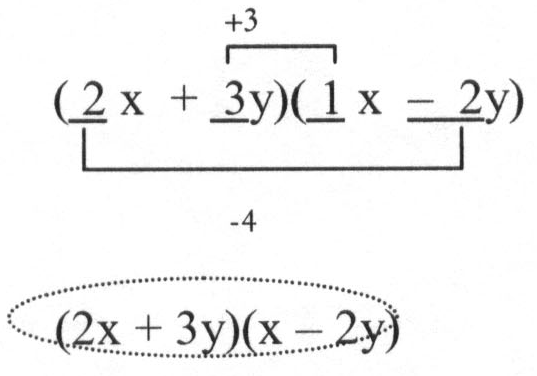
Practice Exercises

Answers to Practice Ecercises