Math 251 Review Topics for Exam 1

Vectors and matrices
Matrices as linear functions - writing a linear function in vector form as
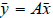
Linear combinations of vectors and the matrix-vector product

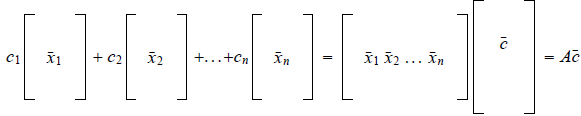where the matrix
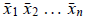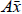A has the vectors as its columns. Conversely: is a combination of the columns
of A with coefficients from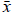

Matrix operations - addition, scalar multiplication, multiplication, and their properties.
Basic matrix algebra. The individual elements of AB as row-column products:

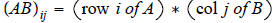
Every column of AB is a combination of the columns of A; every row of AB is a combination
of the rows of B.
Generating AB column by column:  ;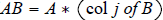
Generating AB row by row: row i of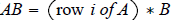
Matrix transpose,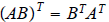

Solution of linear systems:
The matrix form 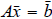of a linear system.
Gauissian elimination to row echelon form, and then to row reduced echelon form.
What row echelon form of A tells you:

the rank, whether solutions always exist, whether solutions are unique
What row echelon form of 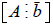tells you: whether a solution of 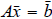exists, also tells
you the row echelon form of A.

Pivot variables and free variables.

How to write the general solution 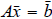of of 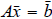in vector form from the row reduced
echelon form of :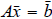

the long way: introduce a parameter for each free variable, solve for each pivot variable
via the equations in the row reduced echelon form, write your answer in vector form

the short way: generate the basic solutions of the homogeneous system 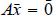using
the row reduced echelon form of A, by in turn setting each free variable to 1 and the others
to zero; then generate a particular solution of 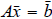using the row reduced echelon form of
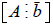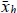by setting all the free variables to zero. Add the general solution of ,
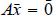obtained via a general linear combination of the basic solutions of 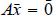, to the particular
solution 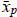of 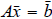to get the general solution

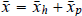
Generating a basic set of solutions of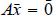

Linear independence: The definition of linear independence. The connection to
homogeneous systems of linear equations. Determining linear independence of a set of
vectors from their row echelon form - determining specific linear combinations from the row
reduced echelon form: expressing one vector as a linear combination of other vectors,
finding a nontrivial linear combination of vectors that gives the zero vector.

Rank of a matrix: Connection of the rank of A with linear systems 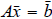, specifically how
the rank of A tells us whether solutions always exist, whether solutions are unique;
connection of rank of A with linear independence of columns of A.

Determinants:
Defining properties of the determinant function
Properties of the determinant:
Effect of row operations on value of the determinant
What the determinant determines: detA ≠ 0 if and only if A ~ I
Determinant of a triangular matrix
Using row operations to find detA
"Pulling out" common factors in a row or column
Interchanging rows
detA^T = detA
The Laplace expansion of detA, the i, j cofactor
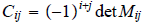
Evaluating a determinant using "pivotal condensation": Successively using row/column
elimination steps so that there is only one nonzero entry in a given column/row and then
expanding.
Determinants with variable entries

Equivalences:
detA ≠ 0
A ~ I (the row reduced echelon form of A is I )
has a solution for each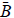
has unique solutions
has only 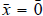as a solution
rank A = n
A is invertible - A^-1 exists - A is nonsingular (these all mean the same thing)
the columns of A are linearly independent

The inverse of a matrix: 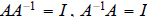(either one implies the other for square
matrices)
Calculating A ^-1 using row operations: 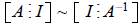. Note that if A ~ I is not true, then
A ^-1 does not exist.
The formula for A^-1 in terms of cofactors: 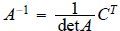where C is the cofactor matrix.
Cramer’s rule:

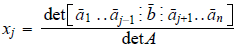If with detA ≠ 0 then where the numerator is the
determinant of the matrix obtained by replacing column j of A by 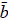, so that 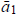represents
column 1 of A and so forth.

Checking an inverse calculation.

Given A^-1 , the unique solution of is 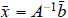(multiply both sides on the left by A^-1
to see that 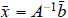must be true)