Pre-Algebra Homework 2 Factors: Solutions

1. Find all of the primes between 70 and 100.

Answer:

First, reject the obvious non-prime numbers. None of the even numbers can be
a prime because they can be divided by two. None of the numbers whose last
digit is 5 is prime because it divides by 5. Every third odd number (check them
of course) can be divided by 3 (see Worksheet 2). So: for the odd numbers
between 70 and 100:

75, 85, 95 are divisible by 5

75, 81, 87, 93, 99 are divisible by 3

This leaves 71, 73, 77, 79, 83, 89, 91, 97. Every 7th odd number divides by 7 -
these numbers are 77 and 91 (77 = 7 × 11 and 91 = 7 × 13.) The next prime
number is 11, but 97÷ 11 = 8 plus remainder 9, i.e. the quotient is smaller than
11. So there are no more prime number factors. The prime numbers between
70 and 100 are 71, 73, 79, 83, 89, 97.

2. Goldbach’s Conjecture says that every even number greater than 2 is the sum of
two primes, though they might be the same prime, and there might be more than
one way to write a number as the sum of two primes. For example, 4 = 2 + 2,
6 = 3 + 3, 8 = 3 + 5, and 10 = 5 + 5 = 3 + 7. “Conjecture” is a fancy word
for “guess”: nobody knows whether Goldbach’s Conjecture is true, but on the
other hand nobody has ever found an exception. Check the Conjecture for even
numbers up to 20.

Answer:

Work this out by subtracting primes one after the other and checking the an-
swer to see if it too is prime. So let’s look at the numbers between 12 and 20.

12 = 2+10 = 3+9 = 5+7 = 7+5
2 and 10 are not primes, 3 and 9 are not primes, but 5 and 7 are primes (and
5+7 is the same as 7+5). So

12 = 5 + 7

and likewise

14 = 3 + 11 = 7 + 7
16 = 3 + 13 = 5 + 11
18 = 5 + 13 = 7 + 11
20 = 3 + 17

so at least as far as 20, this Conjecture is correct.

3. Find the Greatest Common Factors of the following pairs of numbers, first using
Method #1, and then using the Euclidean Algorithm: (a) (16,48) (b) (42,63)
(c) (21,16) (d) (52,39)

Answer:

(a)
16 = 2×2×2×2
48 = 2×2×2×2×3

so the Greatest Common Factor (GCF) is 2×2×2×2 = 16

(b)
42 = 2×3×7
63 = 3×3×7

so the GCF is 3×7 = 21

(c)
21=3×7
16=2×2×2×2

the GCF is 1, i.e. there isn’t one

(d)
52 = 2×2×13
39=3×13

CGF = 13

Now use Euclid’s algorithm:

(a)
16, 48: 48÷16 = 3, remainder 0
so GFC = 16

(b)
42, 63: 63÷42 = 1, remainder 21
42÷21 = 2, remainder 0
So GCF = 21

(c)
21, 16: 21÷ 16 = 1, remainder 7
16÷7 = 2, remainder 2
7÷2 = 3, remainder 1
2÷1 = 2, so we can’t go further

(d)
39,52: 52÷39 = 1, remainder 13
39÷13 = 3, remainder 0

so the GCF = 13

4. Find the Least Common Multiple of the number pairs in the previous problem

Answer

Use the prime factorization from the previous problem:

(a)
16,48: 16 = 2×2×2×2; 48 = 2×2×2×2×3
LCM = 2×2×2×2×3 = 48
The lowest common multiple is 48

(b)
42,63; 42=2×3×7; 63=3×3×7
LCM = 2×3×3×7 = 126

(c)
16,21: 16=2×2×2×2; 21=3×7
LCM = 2×2×2×2×3×7=336

(d)
39,52: 39=3×13; 52=2×2×13
LCM = 2×2×3×13 = 156

5. A mother wishes to divide 6 chocolate bars evenly among 4 children. What is
the smallest total number of pieces needed, into how many pieces must each
bar be broken, and how many pieces does each child receive?

Answer:

Each child can have one whole bar of chocolate, with 2 left over (6÷ 4 = 1,
remainder 2). To share the 2 remaining bars equally among the four children,
each must be broken into two equal halves. There are four halves, so each child
gets one. Each child gets 1 whole bar plus one half bar, two pieces for each
child, 8 pieces in all. If all the pieces have to be the same size, look at the least
common multiple of 6 and 4: 6 = 2×3, 4=2×2. The LCM is 2×2×3 = 12. She
breaks each bar into two equal pieces, 12 pieces in all, and shares them among
the 4 children, who get 3 pieces each.

6. Calculate the prime factors of the following numbers
(a) 1620
(b) 375
(c) 289

Answer

(a)
1620 obviously divides by 10, leaving 162. Sum the integers to get 1+6+2 = 9,
which is divisible by 3. 162 is an even number, so must divide by 2. So far we
have as prime factors 2,5 (10 = 2× 5), 3, and 2. Divide 162 by 2 to get 81, and
81 by 3 to get 27. This is still divisible by 3. 27÷3 = 9. 9÷3 = 3. So the prime
factors of 1620 are: 1620 = 2×2×3×3×3×3×5.

(b)
375 = 5×75 = 5×5×15=5×5×5×3 (and you can check that 375 is divisible by
3 by adding the integers).

(c)
Add the integers to get 19. So 289 is not divisible by 2 (it’s not an even num-
ber), by 3, or by 5 (it doesn’t end in a 5). Try 7: nope. Try 11: nope. 13: nope.
17; yes. 289 = 17×17.

7. President Obama holds a 4th July celebration at the White House for 1289
people. If the invitations come in boxes of 25, each of which costs $40, what is
the cost of the invitations?

Answer

First, divide 1289 by 25 to find out how many boxes are needed: 1289÷25 =
51 with 14 left over. So you have to buy 52 boxes to have enough invitations,
which cost 52× $40 = $2080.

8. Use Method #2 at the end of the class notes:

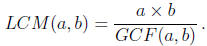
where a and b are two numbers, to calculate the LCM of
(a) 13,4
(b) 10,30
(c) 9,15

Answer

(a)
GCF of 13 and 4 is 1. So

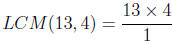
LCM = 13×4/1 = 52

(b)
The GCF of 20 and 30 is 10. So the LCM = (20×30)/10 = 60

(c)

The GCF of 9 and 15 is 3. So the LCM = 9×15/3 = 45

9. Which of the following numbers divides by 3 with no remainder: (a) 246,105
(b) 17 (c) -27 (d) 178,316,166 (e) 29,629,630

Answer

In each case, sum the integers.
(a)
2+4+6+1+5 = 18; 1+8 = 9, which is divisible by 3

(b)
1+7=8, which is not divisible by 3

(c)
2+7 = 9, which is divisible by 3 (note we just need to check the absolute value)

(d)
1+7+8+3+1+6+1+6+6 = 39; 3+9 = 12; 1+2=3. So 178,316,166 is divisible
by 3

(e) 2+9+6+2+9+6+3+0 = 37; 3+7 = 10, which is not divisible by 3.

So the numbers in (a), (c) and (d) are divisible by 3, and the others aren’t.

10. A school PE coach organizes the children into teams to play lacrosse, basketball,
relay racing, and baseball. What is the smallest number of kids at the school
which will allow the school to put each child in a team to play every sport? (there
are 9 players on a baseball team, 4 on a relay racing team, 5 on a basketball
team and 10 on a lacrosse team).

Answer

We want the lowest common multiple of 9, 4, 5 and 10. Do it in pairs. The
LCM of 9 and 4 is 36 (with factors 2, 2, 3, and 3). The LCM of 36 and 5 is
180 (with factors 2,2,3,3,5). The factors of 10 are 2×5. So the LCM of these
four numbers (9, 4, 5 and 10) is 180. If you have 180 kids at the school, each of
them can be on a team to play all four sports.