Math 1200 Real Numbers
Sec. 10.1 Introduction to Real Numbers
The set of real numbers consists of whole numbers, integers,
rational numbers and irrational numbers.
Integer – a positive or negative whole number, or zero
Rational Number – any number that can be written as a
fraction (whole numbers, fractions, decimals that end or
repeat)
Irrational Numbers – numbers whose decimal
representations do not end or repeat (ex: π,
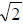 )
)
Comparing Real Numbers
Compare the integers using a < or > symbol:

Absolute value: a number’s distance from zero on
the
number line.
Evaluate:
9. | 5 |
10. | -6 |
11. | -(-8) |
12. | -(7) |
Sec. 10.2 Adding Integers
“Think money”
15 + 9 = 24 “I have 15 and I earn 9 more. Now I have 24”
16 + (-10) = 6 “I have 16 and I spend 10. I still have 6”
(-7) + 2 = -5 “I owe 7 and then I earn 2. I owe only 5.”
(-14) + (-28) = -42 “Two debts add up to more debt!”
Add:
| 1. (-5) + 1 | 2. (-2) + (-5) |
| 3. (-18) + 21 | 4. 19 + (-6) |
| 5. (-4) + 4 | 6. -17 + 4 |
| 7. (-32) + 7 | 8. -41 + (-17) |
| 9. 43 + (-51) | 10. 27 + (-34) |
| 11. 10 + (-12) + 42 + (-34) | 13.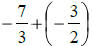 |
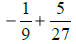 |
|
| 14. 14.123 + (-12.98) |
Opposites: 2 numbers that are the same distance from zero
on the number line.
State the opposite of the number given:
15. 14
16. -45
Evaluate:
17. - (86)
18. - (-13)
Find –x when …
19. x = -16
20. x = 78
Find -(-x) when …
21. x = 9
22. x = -13
Sec. 10.3 Subtracting Real Numbers
“Add the opposite”
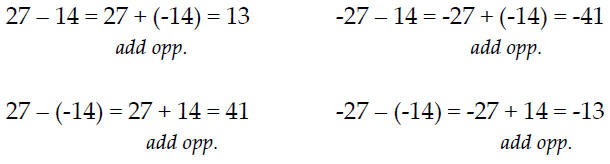
Subtract:
| 1. 41 – (-23) | 2. -11 – (-8) |
| 3. 4 – (-6) | 4. -23 – (-7) |
| 5. 15 – (-6) | 6. 27 – 34 |
| 7. -57 – 31 | 8. -20 – (-30) |
| 9. -25 – (-15) | 10. 50 – (-25) |
| 11. -10 – (-7) – 15 | 12. 35 – 24 – (-16) |
13.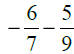 |
14.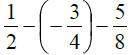 |
15. What is the difference between a summertime high
temperature of 105°F and a wintertime low of -25°F?
Sec. 10.4 Multiplying Real Numbers
Ways to indicate multiplication:
14 x (-3)
14 ·(-3)
14(-3)
Rules:
Multiplication is performed on two numbers at a time.
Multiplying 2 numbers with the same sign gives a
positive answer. 3· 5 = 15 (-4) ·(-7) = 28
Multiplying 2 numbers with different signs gives a
negative answer. -3· 5 = -15
Try these:
| 1. 4 ·(-5) = | 2. (-7)·(-3) = |
| 3. 4· (-3) ·(-2) | 4. 4 ·(-3) ·(-2)· (-1) = |
5.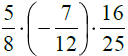 |
Sec. 10.5 Dividing Real Numbers & Order of Operations
Ways to indicate division:
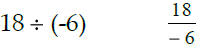
Rules:
Division is performed on two numbers at a time.
Dividing 2 numbers with the same sign gives a
positive answer. -15 ÷ (-3) = 5
Dividing 2 numbers with different signs gives a
negative answer. -28÷ 7 = -4
1. 150 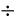 (-3) =
(-3) =
2. -75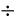 (-3) =
(-3) =
3.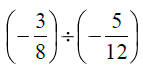
Order of Operations:
1. Inside parentheses
2. Exponents
3. Multiplication/Division
4. Addition/Subtraction
Simplify:
1.2 – (8 – 10)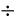 2
2
2. 4 – (-5)· (-2)2
3. 3· 22 + 5 ·(3 + 2) – 17
4. 16 - 4· 8 + 42 – (-18) 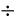 (-9)
(-9)
5. 5 + 7· (3 – 8)2 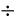 (-14 + 9)
(-14 + 9)
6. (6.2 – 1.3)· (-3)
7.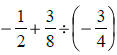
You try these:
| 8. 7(-6) + (-3)3 | 9. -5(3 – 1)2 |
| 10. -2(-3)3 – 8(-1)9 | 11. [ 5 – (-2)]·(3 – 7) |
12. -18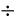 (-3) +
5(-7) (-3) +
5(-7) |
13. [(-7) ·3 + (-6)]
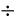 (-9) (-9) |
| 14. (-5 – 3)2 [ -13 – (-5)] | 15. [-9 – (-1)] (5 – 7)4 |




