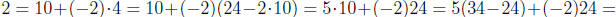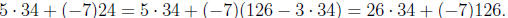Mathematics 541 Homework Solutions

Chapter 0, Problem 1. For n = 8, 12, 20, and 25, find all positive integers less than n and
relatively prime to n.

Answer: The integers 1, 3, 5, and 7 are less than 8 and relatively prime to 8. The integers
1, 5, 7, and 11 are less than 12 and relatively prime to 12. The integers 1, 3, 7, 9, 11, 13,
17, and 19 are less than 20 and relatively prime to 20. The integers 1, 2, 3, 4, 6, 7, 8, 9, 11,
12, 13, 14, 16, 17, 18, 19, 21, 22, 23, and 24 are less than 25 and relatively prime to 25.

Chapter 0, Problem 2. Determine 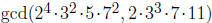and .

An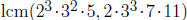swer: We can do this directly by observing exponents on the primes:
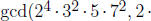
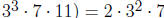and .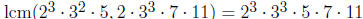

Chapter 0, Problem 3. Determine 51 mod 13, 342 mod 85, 62 mod 15, 10 mod 15, (82 · 73)
mod 7, (51+68) mod 7, (35 · 24) mod 11, (47+68) mod 11.

Answer: We have (using a calculator) 51 mod 13 = 12, 342 mod 85 = 2, 62 mod 15 = 2, 10
mod 15 = 10, (82 · 73) mod 7 = 1, (51+68) mod 7 = 0, (35 · 24) mod 11 = 4, and (47+68)
mod 11 = 5.

Chapter 0, Problem 4. Find integers s and t so that 1 = 7 · s + 11 · t. Show that s and t
are not unique.

Answer: Use the Euclidean algorithm

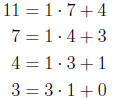
Therefore, we have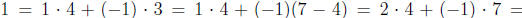
2(11-7)+(-1)(7) = 2 · 11+(-3) · 7. So one set of solutions is s = -3 and t = 2. A full set
of solutions is given by (2 + 7n)11 + (-3 - 11n)7 (though it might be a bit tricky to prove
that this formula will give all solutions).

Chapter 0, Problem 7. Show that if a and b are positive integers, then ab = lcm(a, b) ·
gcd(a, b).

Answer: You can do this problem using the answer in the back of the book, but I prefer not
to use unique prime factorization directly. Set gcd(a, b) = d and lcm(a, b) = m to simplify
notation. We want to prove that ab = dm.

Start by finding integers x and y so that ax +by = d. Multiply this equation by m, and
we have axm+bym = dm. Now, we know that blm, and alax, so ablaxm. Similarly, we can
see that ablbym. Therefore, abldm, so ab ≤ dm.

On the other hand, the number ab/d can be written as 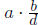, and so ab/d is a multiple
of a. Similarly, ab/d is a multiple of b. Since m is the least common multiple of a and b, we
see that m ≤ ab/d, or md ≤ ab.

Put those two inequalities together, and we get ab = dm.

Chapter 0, Problem 8. Suppose that a and b are integers that divide the integer c. If a
and b are relatively prime, show that ab divides c. Show, by example, that if a and b are not
relatively prime, then ab need not divide c.

Answer: If a and b are relatively prime, we can find integers x and y so that ax + by = 1.
Multiply this equation by c, and we get axc + byc = c. We know that blc, and alax, so
ablaxc. Similarly, we can see that ablbyc. Therefore, ablc.

If a and b are not relatively prime, the conclusion is not true: Let a = 8, b = 12, and
c = 24.

Chapter 0, Problem 10. Let d = gcd(a, b). If a = da' and b = db', show that gcd(a', b') = 1.

Answer: Find integers x and y so that ax + by = d. Divide this equation by d, and we have
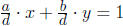, or a'x + b'y = 1. This shows that a' and b' are relatively prime.

Chapter 0, Problem 11. Show that 5n + 3 and 7n + 4 are relatively prime for all n.

Answer: We use long division:

7n + 4 = 1(5n + 3) + 2n + 1
5n + 3 = 2(2n + 1) + n + 1
2n + 1 = 1(n + 1) + n
n + 1 = 1(n) + 1

Since we eventually get 1 as a remainder, we see that 5n + 3 and 7n + 4 must be relatively
prime.

Chapter 0, Problem 16. Show that gcd(a, bc) = 1 if and only if gcd(a, b) = 1 and gcd(a, c) =
1.

Answer: Suppose first that gcd(a, bc) = 1. Find integers x and y so that ax + bcy = 1.
Suppose that dla and dlb. Then dlax and dlbcy, so dl1. Therefore, gcd(a, b) = 1, and a
similar argument shows that gcd(a, c) = 1.

On the other hand, suppose that gcd(a, b) = gcd(a, c) = 1. Find integers x and y so that
ax + by = 1 and integers m and n so that am + cn = 1. Now multiply those two equations,
and we get (ax + by)(am + cn) = 1, or a(xam + xcn + bym) + bc(yn) = 1. This shows that
a and bc are relatively prime.

Chapter 0, Problem 17. Use the Euclidean algorithm to find gcd(34, 126) and write it as a
linear combination of 34 and 126.

Answer: We have



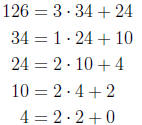
Since 2 is the last non-zero remainder, we see that gcd(34, 126) = 2. Working backwards, we
now see that