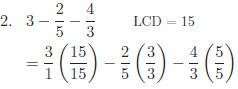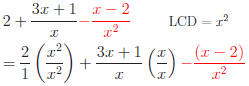Rational Expressions
I. Simplifying
II. Multiplication and Division
III. Addition
IV. Complex Fractions
Answers to Exercises
Your instructor would define a rational expression as "the
quotient of two
polynomials." To you it is the source of that recurring migrane you get whenever
you work with fractions.
To be sucessful with rational expressions you must be proficient in fractional
arithmetic:
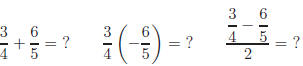
Similar problems involving rational expressions follow the
same principles, only
with algebra concepts intermixed. Do you ll that headache coming on!?
I. Simplifying
Simplifying a rational expression requires finding and removing common
factors that appear in both numerator and denominator. Formally you are
using the fact that 1 ( )=( ): Informally you know it as "cancelling".
For help with factoring, see Review Topic 4.
Below are three fractions, all reduced to lowest terms.
Example: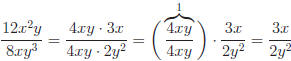
Example: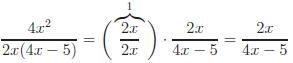
Example: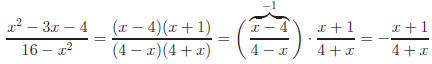
Your own steps may differ from those shown, but there must
be agreement
on the basic concept: simplifying is the removing of factors (not terms) that
are equivalent to 1.
Common Errors:
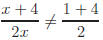 x is a term, not a
factor
x is a term, not a
factor
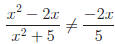 x2 is a
term, not a factor.
x2 is a
term, not a factor.
Repeat after me 10 times: "Factors are cancelled, not terms."
Exercise 1. Simplify each expression.
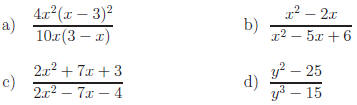 Answers
Answers
II. Multiplication and Division
There are four things to remember when multiplying or dividing fractions.
1) All fractions can be multiplied (common denominators are only neces-
sary when adding.)
2) The product of two fractions is the product of the numerators over the
product of the denominators. 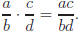
3) To ensure your answer is in lowest terms, cancel common factors
before multiplying.
4) Division is defined in terms of multiplication. a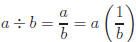
As in simplifying, most of your work comes from factoring. The rest should
be easy.
Example:
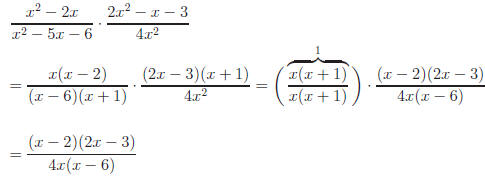
You probably were taught to cancel equal factors.
Repeating the same
example:
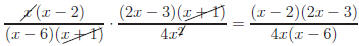
Example: Simplify 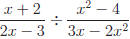
(Remember our comment about division.)
Answer:
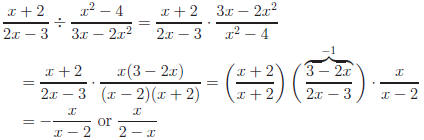
Exercise 2: Perform the indicated operations.
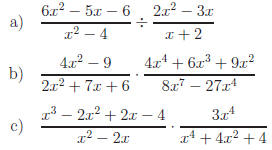 Answers
Answers
III. Addition
Illustration: Compare the following additions; notice the similarity in
steps.
1.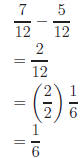
|
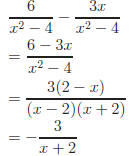
|
(Multiplying by a form of 1 gives fractions a common
denominator and still
maintains equality.)
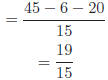 |
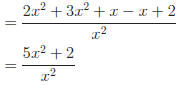 |
With no common factors to cancel, answers are in lowest
terms.
Common Error: Rational expressions oftentimes have polynomials for
numerators. To subtract you must \negate" each term in the numerator.
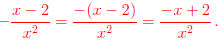
Again, we want to continue to stress that all fractions
follow the same set
of rules.
Guidelines for Adding Rational Expressions
1) Express denominators in factored form.
2) Find the Least Common Denominator (LCD).
3) Convert all fractions into the common denominator by multiplying by
a form of 1.
4) Add.
5) Simplify, i.e. search for common factors to cancel.
Example: Simplify the expression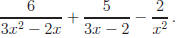
Answer:
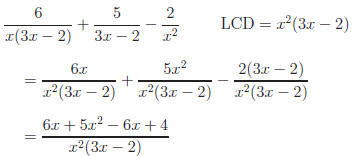
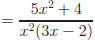
No common factors
guarantees answer in
lowest terms.
Exercise 3: If the following represent denominators, find the LCD.

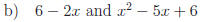 Answers
Answers
Find each sum.

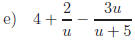 Answers
Answers
IV. Complex Fractions
You are probably thinking, \Aren't all fractions complex?" Yes, but as you
will soon see, some are MORE complex.
A complex fraction contains fractions in its numerator and/or denominator.
Here are two methods you could use to simplify a complex fraction.
Example: 
Method 1: Simplify any sum, then divide.
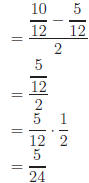 |
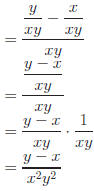
Dividing |
Method 2: Multiply by a form of 1 and cancel.
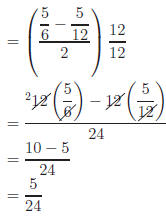 |
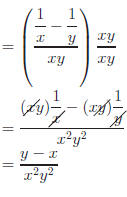 |
Exercise 4: Simplify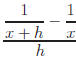 ;
use both methods. Answer
;
use both methods. Answer
Exercise 5: Simplify

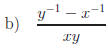
Hint: 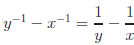 Answers
Answers
Beginning of Topic 108 Skills Assessment
Simplify each expression.
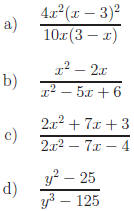
Answers:
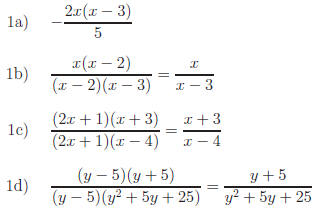
Return to Review Topic
Perform the indicated operations.
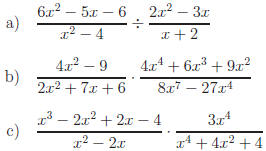
Answers:
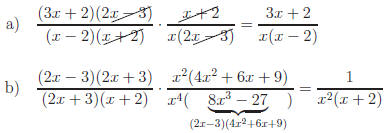
c) Using grouping,
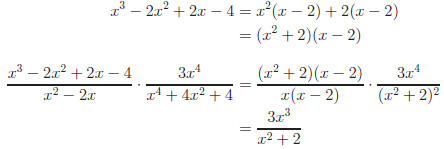
Return to Review Topic
If the following represent denominators, find the LCD.
a) x(x − 3) and x2(x + 3)
b) 6 − 2x and x2 − 5x + 6
c) (x − 1)2; x3 − x and x2
Answers:
a) x2(x − 3)(x + 3)
b) 2(x − 3)(x − 2) Note: 3 − x = −(x − 3)
c) Since x3 − x = x(x − 1)(x + 1), LCD = x2(x − 1)2(x
+ 1)
( d), e), and f) are continued on next page.)
Return to Review Topic
If the following represent denominators, find the LCD.
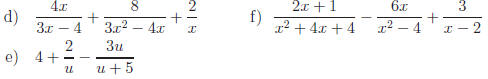
Answers:
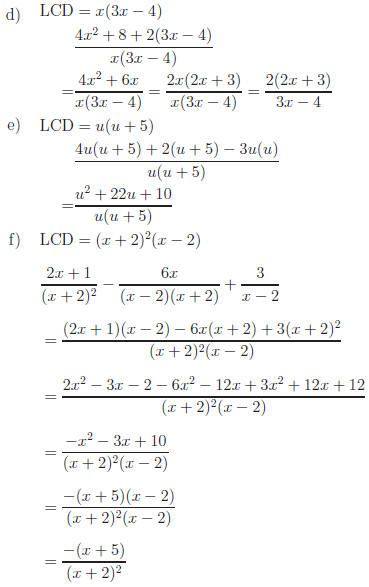 Return to Review Topic
Return to Review Topic
Simplify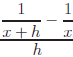 ; use both
methods.
; use both
methods.
Answer:
Method 1:
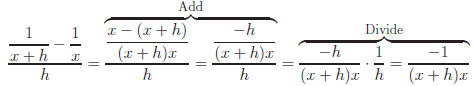
Method 2: If we multiply by 1,
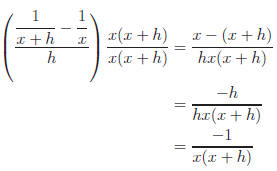 |
Leaving denominator in factored form allows for cancellation. |
Return to Review Topic
Simplify
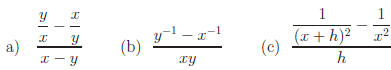
Answers:
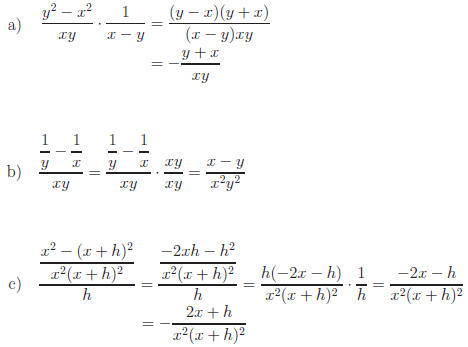
Return to Review Topic