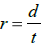Algebra 2 Summer Packet
Vocabulary Review
coefficient - A number multiplied by a variable in a term of an expression.
For example,
in the expression
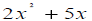 , 2 is the coefficient of x2, and 5 is the
coefficient of x .
, 2 is the coefficient of x2, and 5 is the
coefficient of x .
coordinates - The unique ordered pair of real numbers associated with
each point in a
coordinate plane. The first number of the ordered pair is the x-coordinate; the
second
number is the y- coordinate.
direct variation - A linear function defined by an equation of the form y
= kx, where k is
not equal to zero and remains constant for each ratio y:x of the function.
distributive property - Each term inside a set of parentheses can be
multiplied by a factor
outside the parentheses. For example,
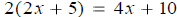
domain - The set of input values of a function for which the function is
defined;
equation – A number sentence that declares the equality of two
expressions; every
equation contains an equal sign separating the left side from the right side
expression – A number phrase consisting of numerals, variables, known
constants, and
mathematical operations
factor - When two or more numbers or variables are multiplied, each of the
numbers or
variables is a factor of the product.
factor of a polynomial – Any of two or more smaller polynomials that, when
multiplied
together, equal the larger polynomial. For example,
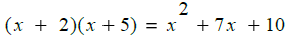
That means that (x + 2) is a factor of the quadratic, and so is (x + 5)
function - A relationship between two variables in which the value of the
dependent
variable is dependent on the value of the control variable. There can only be
one value of
the dependent variable for each value of the control variable.
inequality - A statement formed by placing an inequality sign between two
numerical or
variable expressions
linear inequality - An inequality who graph on a coordinate plane is a region
bounded by
a line, called the boundary line
matrix - An arrangement of numbers in rows and columns.
The number of rows by the
number of columns gives the dimension of the matrix.
quadratic equation - Any equation that can be written in the form ax2 + bx + c =
0, a is
not equal to 0 .
range – the set of output values of a function
root – in a function, any domain (x) value whose output (y) value equals zero; a
solution
to the equation “function = 0”. On a graph, any x-value where the graph crosses
the x
axis
slope-intercept form of an equation - An equation of the form y = mx + b , where
m
represents the slope and b represents the y-intercept of the line. Both values
are
constant.
solution to a system - Values for the variables that make all equations in a
system of
equations true
solution of a system of inequalities - Values for variables that make all
inequalities of the
system of inequalities true
standard form of a linear equation - An equation in the form ax + by = c where
a, b, and
c are integers and a and b are not both zero
system of inequalities - Two or more inequalities in the same variables that
share the
same solution
variation – a specific relationship between the input values (x) and the output
values (y)
of a function. When the product of each x,y pair is constant, the variation is
called
“inverse”; when the ratio of each x,y pair is constant, the variation is
“direct”.
Vertex – the turning point on a graph. To find the vertex of a quadratic
function use the
equations 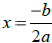 . Determine the output using this input value for the function.
. Determine the output using this input value for the function.
x-intercept - A point where a graph intersects the x-axis; also called a
horizontal intercept
(x,0)
x/y table – a table representing points on a graph, where each row consists of
an x-value
(input) and its corresponding y-value (output). The table also represents
solutions to an
equation that may or may not be a function.
y-intercept - A point where a graph intersects the y-axis; also called a
vertical intercept
(0,y)
zero of a function – same as “root”: an x-value that, when input into a
function, causes
the output (y-value) to equal zero. Any x-intercept of the graph.
Zero property of equality – when two or more factors
multiply to equal zero, one of the
factors must be equal to zero. The equation
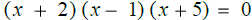 means that x + 2 = 0, or x – 1 = 0, or x + 5 = 0
means that x + 2 = 0, or x – 1 = 0, or x + 5 = 0
Notation
f (x ) represents a function, where the contents of the parentheses – which can
be a
number, a variable, or an expression - are input to the function to create the
output.
x∈R states that the x-values (inputs) of a relation can be any real number, and
the
domain includes all real numbers.
D: [ 2, 20) represents interval notation for the domain. The values inside the
notation
indicate the least and greatest value of the interval, the endpoints. If the [ ]
are used the
interval includes the endpoints, and if ( ) are used, the interval does not
include the
endpoints identified. The domain and range are often identified using interval
notation.
The notation identified indicates the domain is all real numbers from 2 through
20
including 2 but not 20. An important note is that the infinity symbol is ALWAYS
preceded
or followed by ( or ).
D: 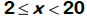 represents inequality notation for the domain and means the domain is
all
represents inequality notation for the domain and means the domain is
all
real numbers from 2 through 20 including 2 but not 20.
Evaluating Expressions and Scientific Notation
Evaluate if a = 5, b = -7, and c = 8
1.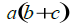
2.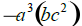
3.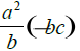
4.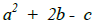
5.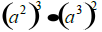
Write your answer as an exponent.
6.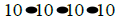
7.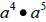
8.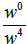
9.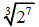
10. Write in scientific notation:
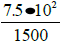
Order of Operations and Statistics
Calculate according to the order of operations.
11.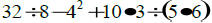
12. 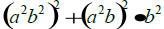
13. Solve 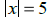
14. Graph 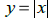
15. Graph the quadratic function
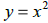 . Use an x/y table of values for your input
to
. Use an x/y table of values for your input
to
determine your output values. Identify the roots, y-intercept, and vertex.
16. Graph: 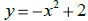 . Compare your graph to problem
15. Using full
. Compare your graph to problem
15. Using full
sentences identify similarities and differences between the graphs and their
equations.
17. Graph: 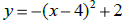 . Compare this graph with Problem
16. Using full
. Compare this graph with Problem
16. Using full
sentences, identify similarities and differences between the graphs and their
equations.
18. Use the given data set to find the mean, median, and mode.
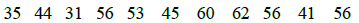
Solving Equations - Notes
Linear equations
| Example 1: | Example 2: |
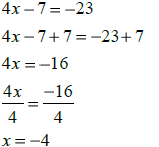 |
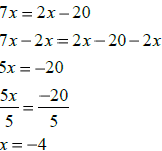 |
Systems of Equations
Solve:
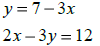
Solution:
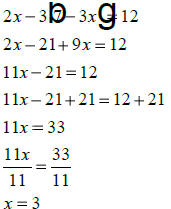 |
substitute |
| distribute | |
| combine like terms | |
| add 21 to both sides | |
| simplify | |
| divide both sides by 11 | |
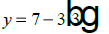 |
substitute to find the value of y |
The solution to the system is 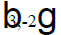
Solving for a variable
Solve: 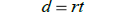 for r
for r
Solution:
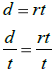 divide both sides by t
divide both sides by t