Math Content by Strand

Fractions /Rational Numbers

Grades K-1
Although the Grade 2 unit is the first unit in the rational numbers strand, students develop ideas about
fractions informally both outside of school and through activities in Kindergarten and Grade 1. For
example, as kindergarteners and first graders use the Shapes software, and work on activities such as Fill
the Hexagons and Pattern Block Fill-In, they begin to find relationships among the pattern block
shapes–two trapezoids equal one hexagon (or a trapezoid is 1/2 of a hexagon), six triangles equal one
hexagon, three triangles equal one trapezoid, etc.

Young students also encounter fractions as they measure and compare quantities or lengths. The first
grade curriculum capitalizes on this in the unit Fish Lengths and Animal Jumps (Measurement), asking
students to consider lengths that fall between whole numbers of units.

Grade 2

Second graders develop an understanding of what fractions are and how they can be used to name
quantities. They learn that fractions are quantities that are equal parts of a whole whether the whole is a
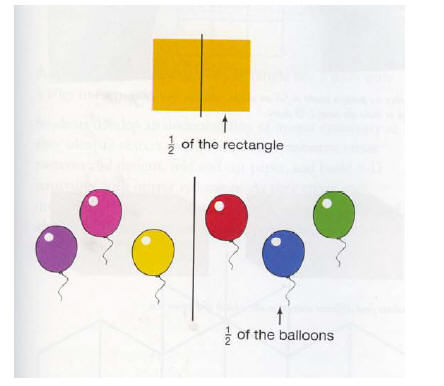
single object or a set of objects. Students work with 1/2, 1/3, 1/4, 2/3, 2/4, and 3/4 of single objects such
as blocks, rectangles, squares and flags. They work with 1/2, 1/3, and ¼ of sets of objects such as
balloons, sandwiches and other objects shared among a group of people.

Students learn how fractions are expressed in words—one half, two thirds—and represented using
numbers—for example, 1/2, 2/3. They learn that the denominator represents the number of equal parts
in the whole and that the numerator represents the number of the equal parts being considered, though
they are not expected to use the words denominator and numerator when describing fractions. Students
also learn the notation for mixed numbers through dividing sets. For example, if two girls share three
sandwiches, each girl gets 1 1/2 sandwiches.

Emphases

What Fractions Are
• Understanding fractions as equal parts of a whole
• Using terms and notation

Benchmarks
• Identify 1/2, 1/3, and 1/4 of a region
• Find 1/2 of a set of objects
• Recognize that a fraction divides the whole into equal parts

Grade 3

Students use a variety of contexts to understand, represent, and combine fractions. These include
rectangles representing “brownies,” hexagonal pattern block “cookies,” and groups of objects.

Students work with halves, fourths, eighths, thirds, and sixths as they learn how fractions represent equal
parts of a whole. They learn the meanings of the numerator and denominator of a fraction, so that when
comparing unit fractions (fractions with a numerator of 1), they understand that the larger the
denominator the smaller the part of the whole: 1/6 is smaller than ½ of the same whole. Students also
gain experience with common equivalencies, for example, that 3/6 and 2/4 are both equal to 1/2. Using
these equivalents in contexts, students find combinations of fractions that are equivalent to a whole or to
another fraction. For example,

1/2 + 2/6 + 1/6 = 1
1/3 + 1/6 = 1/2

Students are introduced to decimal fractions (0.50 and 0.25), using the context of money, and gain
familiarity with fraction and decimal equivalents involving halves and fourths.

Emphases
Rational Numbers

• Understanding the meaning of fractions (halves, fourths, eighths, thirds, sixths) and decimal
fractions (0.50, 0.25) as equal parts of a whole (an object, an area, a set of objects)
• Using representations to combine fractions (halves, fourths, eighths, thirds, and sixths)

Benchmarks

• Divide a single whole or a quantity into equal parts and name those parts as fractions or mixed
numbers
• Identify equivalent fractions (e.g.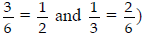

• Find combinations of fractions that are equal to 1 and to other fractions (e.g.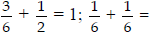

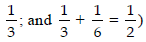
Grade 4

The major focus of the work on rational numbers in Grade 4 is on building students’ understanding of
the meaning, order, and equivalencies of fractions and decimals. Students continue to focus on the
meaning of fractions as equal parts of a whole. They extend their images of equal parts to accommodate
fractions that are greater than 1. Students work with fractions in the context of area (equal parts of a
rectangle), as a group of things (e.g., a fractional part of the class), and on a number line. They work
with fractions that represent halves, thirds, fourths, fifths, sixths, eighths, tenths, and twelfths.

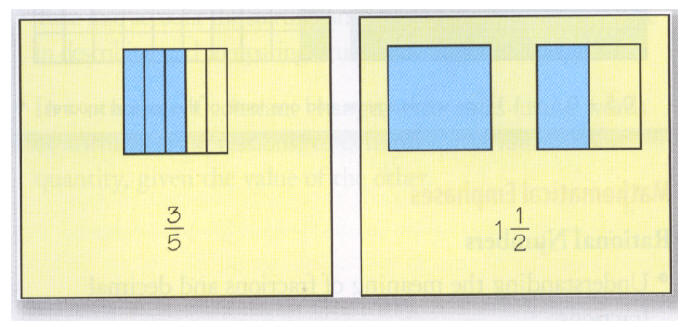
Students are introduced to decimal fractions in tenths and hundredths as an extension of the place value
system they have studied for whole numbers. They relate decimals to equivalent decimals and fractions
(for example, when they represent 0.25 as part of a rectangle, they can see how it is equal to ¼ and to 2
½ tenths). Students draw on their mental images of fractions and decimals and on their knowledge of
fraction and decimal equivalencies and relationships to reason about fraction comparisons, to order
fractions on a number line, and to add fractions and decimals using representations.

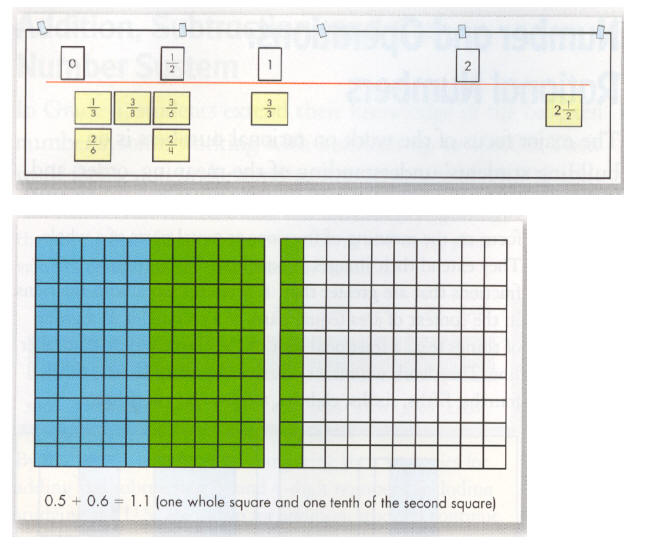
Emphases

Rational Numbers
• Understanding the meaning of fractions and decimal fractions
• Comparing the values of fractions and decimal fractions

Computation with Rational Numbers
• Using representations to add rational numbers

Benchmarks
• Identify fractional parts of an area
• Identify fractional parts of a group (of objects, people, etc.)
• Read, write, and interpret fraction notation
• Order fractions with like and unlike denominators
• Read, write, and interpret decimal fractions in tenths and hundredths

Grade 5
The major focus of the work on rational numbers in grade 5 is on understanding relationships among
fractions, decimals, and percents. Students make comparisons and identify equivalent fractions,
decimals, and percents, and they develop strategies for adding and subtracting fractions and decimals.

In a study of fractions and percents, students work with halves, thirds, fourths, fifths, sixths, eighths,
tenths, and twelfths. They develop strategies for finding percent equivalents for these fractions so that
they are able to move back and forth easily between fractions and percents and choose what is most
helpful in solving a particular problem, such as finding percentages or fractions of a group.

Students use their knowledge of fraction equivalents, fraction-percent equivalents, the relationship of
fractions to landmarks such as ½, 1, and 2, and other relationships to decide which of two fractions is
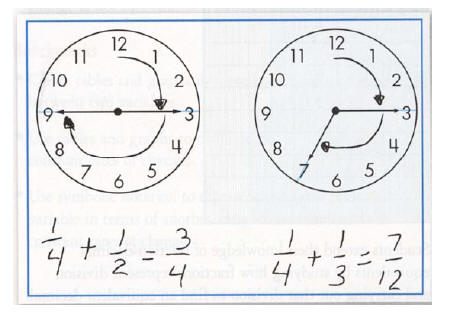
greater. They carry out addition and subtraction of fractional amounts in ways that make sense to them
by using representations such as rectangles, rotation on a clock, and the number line to visualize and
reason about fraction equivalents and relationships.

Students continue to develop their understanding of how decimal fractions represent quantities less than
1 and extend their work with decimals to thousandths. By representing tenths, hundredths, and
thousandths on rectangular grids, students learn about the relationships among these numbers—for
example, that one tenth is equivalent to ten hundredths and one hundredth is equivalent to ten
thousandths—and how these numbers extend the place value structure of tens that they understand from
their work with whole numbers.

Students extend their knowledge of fraction-decimal equivalents by studying how fractions represent
division and carrying out that division to find an equivalent decimal.

They compare, order, and add decimal fractions (tenths, hundredths, and thousandths) by carefully
identifying the place value of the digits in each number and using representations to visualize the
quantities represented by these numbers.

Emphases

Rational Numbers
• Understanding the meaning of fractions and percents
• Comparing fractions
• Understanding the meaning of decimal fractions
• Comparing decimal fractions

Computation with Rational Numbers
• Adding and subtracting fractions
• Adding decimals

Benchmarks
• Use fraction-percent equivalents to solve problems about the percentage of a quantity
• Order fractions with like and unlike denominators
• Add fractions through reasoning about fraction equivalents and relationships
• Read, write, and interpret decimal fractions to thousandths
• Order decimals to the thousandths
• Add decimal fractions through reasoning about place value, equivalents, and representations