Math 601 Test 1 Solutions

Instructions: This is an open notes exam. No additional resources (web sites, etc.)
or people (classmates, friends, famous or infamous mathematicians, lowly Lynch-
burg College mathematicians (other than me), etc.) may be used in the completion
of this exam.

I. Decide whether each of the following is true or false. If the statement is true,
prove it. If it is false, give a counter-example.

(1) If a ≤ b and c ∈ R, then ac ≤ bc.
False, this only works if c ≥ 0. Let a = 2 and b = 3. Then we have a ≤ b
but for c = -1 we have -3 ≤ -2, i.e. bc ≤ ac.

(2) For each x ∈ Z there is a unique element x^-1 ∈ Z such that xx^-1 = 1.
False, if x = 0 ∈ Z, then x^-1 does not exist. Also if x = 2 ∈Z, then


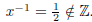
(3) If x ∈ R is not the root of any polynomial with integer coefficients, then


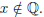
True.

Proof. We will prove the contrapositive. That is, if x ∈ Q then x is the
root of a polynomial with integer coefficients. Suppose x∈ Q. Then we can
write 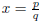where p, q ∈ Z with q ≠ 0. Then x is a root of the polynomial
qx - p which has integer coefficients.

(4) If 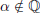, then .

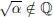True.

Proof. To prove the contrapositive, suppose 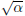∈ Q. Then since Q is
closed under multiplication we have .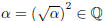

(5) If x ∈ R is an algebraic number, then it is rational.

False. Let x = 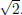Then x is a root of x² - 2 which has integer coeffi-
cients, but

II. Prove each of the following.

(1) Let α be any irrational number and r be any nonzero rational number.
Prove that the addition, subtraction, multiplication, and division of r and
α yield irrational numbers. That is, Prove that α + r, α - r, r - α, rα,
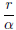
and 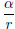are all irrational numbers.

Proof. Let α be irrational and r ∈ Q. Suppose 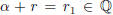. Then
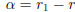. Since Q is closed under addition, 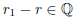which contradicts


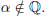
The other cases are similar since the rationals are closed under all basic
operations .

(2) Let x be an algebraic number and n ∈ N. Prove that 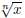is also algebraic.

Proof. Since x is algebraic, it is a root of

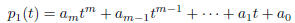
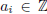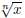where   for i = 0, 1, ... , m. Then is a root of the polynomial
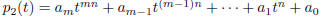. This is because

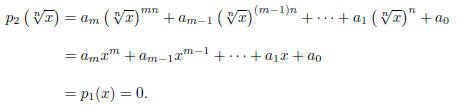
(3) Given that α and β are irrational, but α + β is rational, prove that α - β
and α + 2β are irrational.

Proof. Let 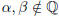with 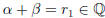. Suppose 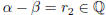. Then

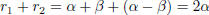and.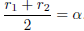

Since Q is closed under the basic operations 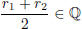which contradicts


Now suppose 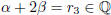. Then



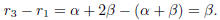
Since Q is closed under the basic operations this contradicts .

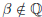(4) Let a, n ∈N. Prove that 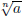is either irrational or an integer. (Hint: it's
algebraic.)

Proof. Let a, n ∈ N. Then 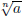is a root of the polynomial p(t) = tⁿ - a
which has integer coefficients. By the Rational Zeros Theorem the only
possible rational roots of this are the integer divisors of a. If 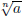is among
these divisors, then 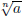is an integer. If 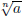is not among these divisors,
then it is irrational.

(5) Let a, b ∈ R. Prove that  lbl  < a if and only if -a < b < a.

Proof. Suppose  lbl  < a. We need to show two inequalities: -a < b
and b < a. The first can be rewritten as -b < a. Recall that -b ≤  lbl
and b ≤  lbl . Now since  lbl  < a we have, -b ≤  lbl  < a which is the first
inequality. Similarly, b ≤  lbl  < a which is exactly the second inequality.

Now suppose -a < b < a. In order to show that  lbl  < a we must
show that b < a and -b < a (since  lbl  = b or  lbl  = -b). By assumption
b < a which is the first required inequality. We also know -a < b, which
can be rewritten as -b < a, which is the second required inequality.