Systems of Linear Equations
6.1 Solve Systems of Linear Equations by Graphing
6.2 Solve Systems of Linear Equations by the Substitution
Method
6.3 Solve Systems of Linear Equations by the Addition
(Elimination) Method
6.4 Application Problem Involving Two Equations and Two
Variables.
6.1 Solve Systems of Linear Equations by Graphing
A system of equations is a set of two or more
equations
considered together. A solution to a system of equations in two
variables is an ordered pair that is a solution to every equation in
the system.
Example 1 Solutions to a System of Equations
a. Is (2, -1) a solution to the system
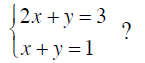
b. Is (1, -3) a solution to the system
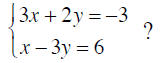
Recall: All ordered pair solutions to an equation form
the graph
of an equation in two variables.
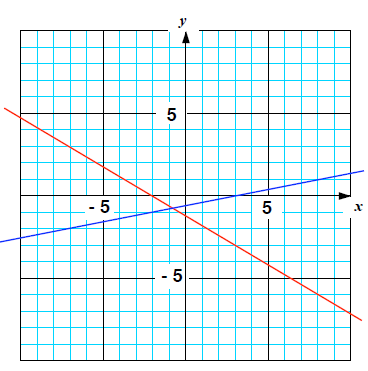
Example 2 Solve by the Graphing Method
a. Solve by graphing
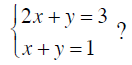
b. What is the point of intersection of
the two graphs?
c. What is the solution to the system of
equations?
d. What is the relationship between the point(s) of
intersection and
the solution(s) to the system of equations.
The Solution Set to a Linear System of Two Equations
in Two Variables has Three Possible Outcomes . . .
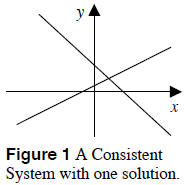
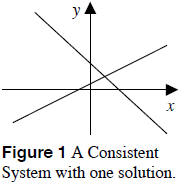
1. One Solution See Figure 1. The lines
intersect at one point and the solution set
contains only one point. A system of linear
equations with at least one solution is
called a consistent system. The solution to
the system is expressed as an ordered pair
(a,b) .
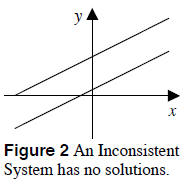
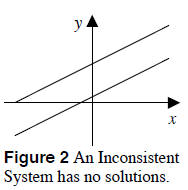
2. No Solutions See Figure 2. The lines
are distinct and parallel, and never
intersect. Therefore, there is no solution.
A linear system whose solution set is
empty is called an inconsistent system.
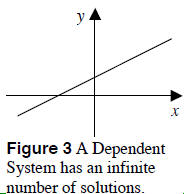
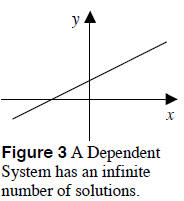
3. Infinite Number of Solutions See
Figure 3. The lines lie on top of each other,
are not distinct, and have an infinite number
of points of intersection. Therefore, the
system of equations has infinite solutions.
This is called a dependent system.
Example 3 An Inconsistent System means the system
has no solution and the two lines are parallel.
Solve by graphing
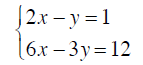
Example 4 A Dependent System means the two lines are
the same.
Solve by graphing
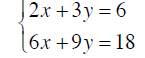
Example 5
Solve by graphing
Example 6
Solve by graphing
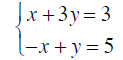
Example 7
Solve by graphing
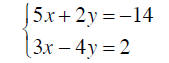
Example 8
Solve by graphing
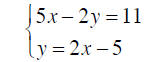
6.2 The Substitution Method
Solve
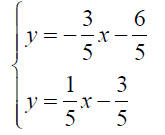
Algebraic Methods to Solve Systems of Equations
The solution to the above system is (-3/4, -3/4). The graphing
method only works well when the ordered pair solution contains
only integer numbers. Therefore, we need an algebraic method for
solving systems of equations. The two algebraic methods we are
going to learn are the Substitution Method and the Addition
(Elimination) Method.
Substitution Method
1. Isolate one variable in one of the given equations.
2. Substitute the equation from step 1 into the other equation and
solve for the one variable remaining in that equation.
3. Use the equation from step 1 to find the value of the other
variable.
4. Write your solution as an ordered pair.
5. Check the solution.
Example 1
Solve by substitution
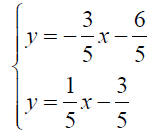
Example 2
Solve by substitution
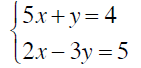
Example 3
Solve by substitution
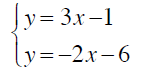
Example 4
Solve by substitution
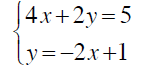
Example 5
Solve by substitution
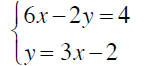
Two exceptions that may occur when using the
Substitution Method
Inconsistent System If at some point in working the
algebra in
step 2 you get an untrue statement, such as 3 = 5, then you have an
inconsistent system. That is, the graphs of the lines are parallel
and never intersect.
Dependent System If at some point in working the
algebra in
step 2 you get a worthless but true statement, such as 4 = 4, then
you have a dependent system. That is, the graphs of the lines lie
on top of each other and the system has an infinite number of
solutions (points of intersection).
The Solution Set to a Linear System of Two Equations
in Two Variables has Three Possible Outcomes . . .
1. One Solution See Figure 1. The lines
intersect at one point and the solution set
contains only one point. A system of linear
equations with at least one solution is
called a consistent system. The solution to
a consistent system is expressed as an
ordered pair (a,b) .
2. No Solutions See Figure 2. The lines
are distinct and parallel, and never
intersect. Therefore, there is no solution.
A linear system whose solution set is
empty is called an inconsistent system. The
Elimination and Substitution methods
produce a false statement, such as 4 = 0.
3. Infinite Number of Solutions See
Figure 3. The lines lie on top of each other,
are not distinct, and have an infinite number
of points of intersection – every point on
the line. Therefore, the system of equations
has an infinite number of solutions. This is
called a dependent system. The Elimination
and Substitution methods produce a true
statement, such as 3 = 3.
Example 6
Solve by substitution
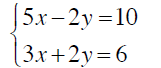
Example 7
Solve by the substitution method
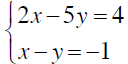
6.3 The Addition (Elimination) Method
Example 1
Solve by the Addition Method
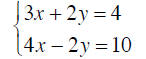
Recall If c ≠ 0 and a = b , then ac = bc .
This means you can multiply both sides of an equation by
the same non-zero number without changing the solution
set (i.e. the graph) of the equation. The modified system
of equations is equivalent to the original system.
Example 2
Solve by the Addition Method
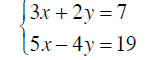
Example 3 Both equations may have to be changed
Solve by the Addition Method
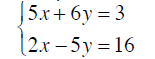
Note To use the addition method both equations must be
written so that all variable terms are on one side of
each equation and the constant term is on the other
side.
Example 4
Solve by the Addition Method
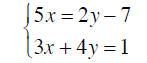
Example 5
Solve by the Addition Method
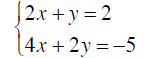
Example 6
Solve by the Addition Method
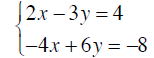
Example 7
Solve by the Addition Method
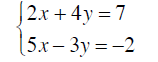
Example 8
Solve by the Addition Method
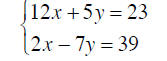
6.4.1 Wind-Current and Water-Current Problems
Example 1
Flying with the wind, a plane can fly 750 miles in 3 hours. Against
the wind, the plane can fly the same distance in 5 hours. Find the
rate of the plane in calm air and the rate of the wind.
General Strategy
1. Choose one variable to represent the rate of the object in a calm
condition and a second variable to represent the rate of the
wind or current.
let
p = the rate of the plane in calm air
w = rate of the wind
so that
p + w = rate of the plane traveling with the wind
p - w = rate of the plane traveling against the wind
2. Use the expressions from step 1, as well as the time
traveled
with and against the wind, to get expressions for the distances
traveled with and against the wind. Recall:
Rate ·Time = Distance is used to determine the expression
for the
distance traveled. Organize the data in a table.
| Trip | Rate | . | Time | = | Distance |
| With the wind | . | = | |||
| Against the wind | . | = |
3. Write a system of equations that models the problem.
4. Solve the system of equations and answer the question.
Example 2
A 600 mile trip from one city to another takes 4 hours when the
plane is flying with the wind. The return trip against the wind
takes 5 hours. Find the rate of the plane in still air and the rate of
the wind.
Example 3
A canoeist paddling with the current can travel 24 miles in 3 hours.
Against the current, it takes 4 hours to travel the same distance.
Find the rate of the canoeist in calm water and the rate of the
current.
6.4.2 Other Application Problems Involving Two
Equations and Two Unknowns
Example 4
A jeweler purchased 5 oz of a gold alloy and 20 oz of a silver alloy
for a total cost of $700. The next day, at the same prices per
ounce, the jeweler purchased 4 oz of the gold alloy and 30 oz of
the silver alloy for a total cost of $630. Find the cost per ounce of
the silver alloy.
Example 5
A store owner purchases 20 incandescent light bulbs and 30
fluorescent bulbs for $40. A second purchase, at the same prices,
included 30 incandescent light bulbs and 10 fluorescent bulbs for
$25. Find the cost of each type of bulb.
Example 6
Two coin banks contain only dimes and quarters. In the first bank,
the total value of the coins is $3.90. In the second bank, there are
twice as many dimes as in the first bank and one-half the number
of quarters. The total value of the coins in the second bank is
$3.30. Find the number of dimes and quarters in the first bank.




