Scientific Notation

Scientific notation provides a convenient way of depicting very large or very small numbers. The notation xⁿ means multiply the number x together n times. The number n is known as the exponent. For example:

8² = 8 x 8 = 64
10³ = 10 x 10 x 10 = 1000
10⁶ = 10 x 10 x 10 x 10 x 10 x 10 = 1,000,000

If the exponent is a negative number, then one must note the following:

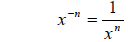
Therefore, the following examples become:

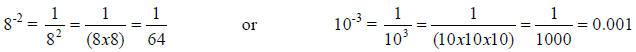
This notation works with the "UNITS" also (not just numbers). For example, a unit that you are familiar with is miles per hour (mph). If you are driving 75 mph this is mathematically written as:

75 mi/hr or is written as 75 mi hr^-1using the notation above.

Through the use of exponents, very large or small numbers can be expressed in a less cumbersome manner by using scientific notation. The following numbers are expressed in their scientific notation form:

1,000,000 = 1 x 10⁶
1,000 = 1 x 10³
10 = 1 x 10¹
0.1 = 1 x 10^-1
0.001 = 1 x 10^-3
0.000001 = 1 x 10^-6

In the number 5.6 x 10⁹, there are two parts. "5.6" is called the base and "9" (in 10⁹) is the exponent.

To write a number in scientific notation:
For numbers greater than 1

Put the decimal after the first digit.
Let’s try the number 123,000,000,000

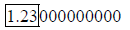
The non-zero values give you the base number. Here the base is 1.23

Then, to find the exponent, count the number of places from the decimal to the end of the number.
In 1.2 3,0 0 0,0 0 0,0 0 0 there are 11 places. Finally, drop all of the zeros. Therefore we write 123,000,000,000 as:

1.23 x 10¹¹

Other examples: 8,000 can be written as 8 x 10³ and 4,253 can be written as 4.253 x 10³.

For numbers less than 1

For example 0.000478
We want to move the current decimal to the right just past the first non-zero number (in this case, after the 4). We need to count the number of places we move to do this.

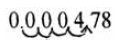
moved the decimal 4 places. Therefore the number in scientific notation is expressed as:

4.78 x 10^-4

To convert back from scientific notation:
For numbers greater than 1

These have positive exponents, so we will be moving the decimal to the right…
So, 9.342 x 10⁶ = 9 3 4 2 Filling in the zeros we get 9342000.0 = 9,342,000

For numbers less than 1

These have negative exponents, so we will be moving the decimal to the left…

So, 3.2 x 10^-3 would be shown as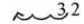which is 0.0032

Other notations…
Exponents are often expressed using other notations. The number 123,000,000,000 can also be written as:
1.23E+11 or as 1.23x10¹¹

For small numbers we use a similar approach. Numbers less than 1 will have a negative exponent.
0.001 is written as or 1.0x10^-3 or 0.1E−3

Try these practice problems to get familiar with the technique.

4.3 x 10^-3 =

6.334 x 10⁵ =

5.56 x 10⁷ =

9 x 10^-7 =

23,000 =

0.658 =

0.0000394 =

344,000,000 =

0.32 x 10^-2 =

0.0041 x 10² =

20 =