Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

IS THIS LONG DIVISION,TOO?

In a certain country, students learn to divide using the following algorithm:

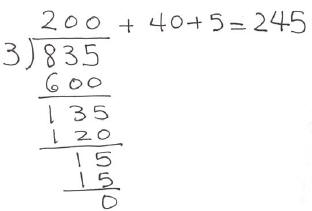
1. How would a student in this country calculate 752 ÷ 3?
2. Someone started his calculation this way:

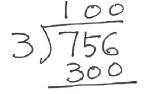
Complete this problem.
3. Use this algorithm to calculate 483 ÷ 13.

Discussion, Suggestions and Possible Solutions

This particular algorithm is similar to the long division algorithm we have investigated in this unit previously. However, since the quotient is written as an addition sentence, it allows a little more flexibility in carrying out the division. In

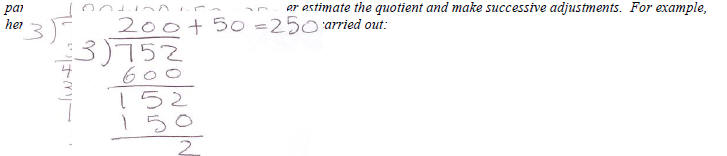
As you can see, with this algorithm, students do not have to start with the best initial estimate. In (b), students are asked to complete the division even when the initial estimate is not the optimal one. Here is one possible answer:

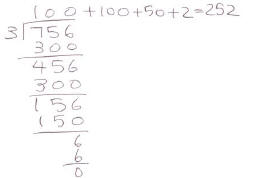
Another flexibility that this algorithm offers is to interpret the process with the measurement division, which may be more useful when the divisor becomes large. For example, in 483 ÷ 13 (problem c), you can interpret the problem, “How many groups of 13 can we make with 483?” Here is one way this division may be carried out:

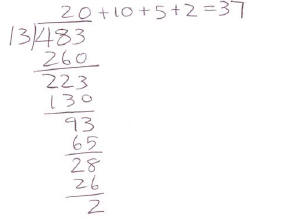
Each step may be interpreted this way:
• We can make at least 20 groups of 13, which will use up 260 of 483, leaving 223.
• With 223, we estimate we can make at least 10 groups of 13. which uses up 130. Now we are left with 93.
• We estimate that we can make at least 5 groups of 13. We still have 28 left.
• We can make 2 more groups of 13.
• What’s left now, 2, is too small to make another group of 13, so this is the remainder.

Extension:
Provide additional problems involving 2-digit divisors. As students gain more proficiency, their estimate will become more accurate.

Home