Functions

2.2.1. Correspondences. Suppose that to each element of a set
A we assign some elements of another set B. For instance, A = N,
B = Z, and to each element x ∈N we assign all elements y ∈Z such
that y^2 = x (fig. 2.8).

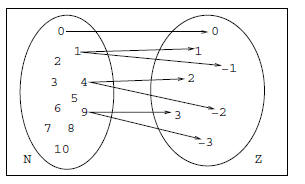
Figure 2.8. Correspondence

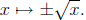
This operation is called a correspondence.

2.2.2. Functions. A function or mapping f from a set A to a set
B, denoted f : A -> B, is a correspondence in which to each element
x of A corresponds exactly one element y = f(x) of B (fig. 2.9).

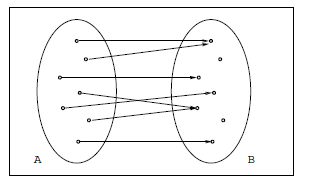
Figure 2.9. Function.

Sometimes we represent the function with a diagram like this:

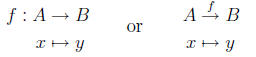
For instance, the following represents the function from Z to Z
defined by f(x) = 2x + 1:

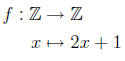
The element y = f(x) is called the image of x, and x is a preimage
of y. For instance, if f(x) = 2x + 1 then f(7) = 2 · 7 + 1 = 15. The
set A is the domain of f, and B is its codomain. If 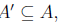the image
of A' by f is f(A') = {f(x) | x ∈A'}, i.e., the subset of B consisting
of all images of elements of A'. The subset f(A) of B consisting of
all images of elements of A is called the range of f. For instance, the
range of f(x) = 2x + 1 is the set of all integers of the form 2x + 1 for
some integer x, i.e., all odd numbers.

Example: Two useful functions from R to Z are the following:

1. The floor function:
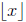= greatest integer less than or equal to x .

For instance:

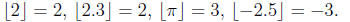
2. The ceiling function:
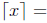least integer greater than or equal to x .
For instance:

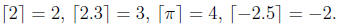
Example: The modulus operator is the function mod : Z×Z⁺ -> Z
defined:

x mod y = remainder when x is divided by y.

For instance 23 mod 7 = 2 because 23 = 3·7+2, 59 mod 9 = 5 because
59 = 6 · 9 + 5, etc.

Graph: The graph of a function f : A -> B is the subset of A × B
defined by G(f) = {(x, f(x)) | x ∈A} (fig. 2.10).

2.2.3. Types of Functions.

1. One-to-One or Injective: A function f : A -> B is called one-to-
one or injective if each element of B is the image of at most
one element of A (fig. 2.11):

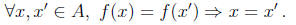
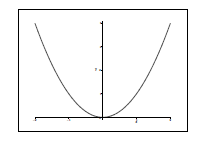
Figure 2.10. Graph of f(x) = x^2.

For instance, f(x) = 2x from Z to Z is injective.

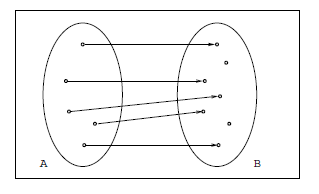
Figure 2.11. One-to-one function.

2. Onto or Surjective: A function f : A -> B is called onto or
surjective if every element of B is the image of some element of
A (fig. 2.12):

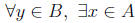such that y = f(x) .

For instance, f(x) = x^2 from R to 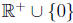is onto.

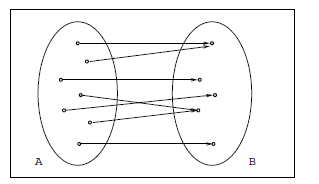
Figure 2.12. Onto function.

3. One-To-One Correspondence or Bijective: A function f : A ->
B is said to be a one-to-one correspondence, or bijective, or a
bijection, if it is one-to-one and onto (fig. 2.13). For instance,
f(x) = x + 3 from Z to Z is a bijection.

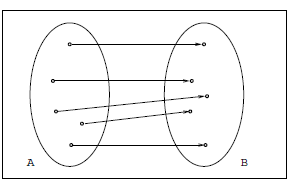
Figure 2.13. Bijection.

2.2.4. Identity Function. Given a set A, the function 1_A : A ->
A defined by 1_A(x) = x for every x in A is called the identity function
for A.

2.2.5. Function Composition. Given two functions f : A -> B
and g : B -> C, the composite function of f and g is the function
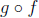: A -> C defined by (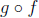)(x) = g(f(x)) for every x in A:

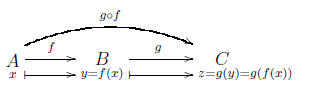
For instance, if A = B = C = Z, f(x) = x + 1, g(x) = x^2, then
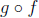()(x) = f(x)^2 = (x+1)^2. Also (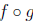)(x) = g(x)+1 = x^2 +1 (the
composition of functions is not commutative in general).

Some properties of function composition are the following:

1. If f : A -> B is a function from A to B, we have that

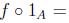
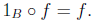
2. Function composition is associative, i.e., given three functions

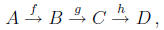
we have that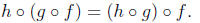

Function iteration. If f : A -> A is a function from A to A, then
it makes sense to compose it with itself: 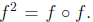For instance, if
f : Z -> Z is f(x) = 2x + 1, then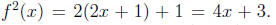
Analogously we can define 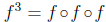, and so on,

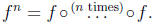
2.2.6. Inverse Function. If f : A -> B is a bijective function, its
inverse is the function f⁻¹ : B -> A such that f⁻¹(y) = x if and only
if f(x) = y.

For instance, if f : Z -> Z is defined by f(x) = x + 3, then its
inverse is f⁻¹(x) = x − 3.

The arrow diagram of f⁻¹ is the same as the arrow diagram of f
but with all arrows reversed.

A characteristic property of the inverse function is that
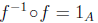
and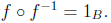

2.2.7. Operators. A function from A × A to A is called a binary
operator on A. For instance the addition of integers is a binary operator
+ : Z × Z -> Z. In the usual notation for functions the sum of
two integers x and y would be represented +(x, y). This is called prefix
notation. The infix notation consists of writing the symbol of the binary
operator between its arguments: x+y (this is the most common).
There is also a postfix notation consisting of writing the symbol after
the arguments: x y +.

Another example of binary operator on Z is (x, y) -> x · y.

A monary or unary operator on A is a function from A to A. For
instance the change of sign x -> −x on Z is a unary operator on Z. An
example of unary operator on R* (non-zero real numbers) is x -> 1/x.