- Home
MATH 20 INTEGRAL REVIEW
0.1. Main idea. FTC implies: for every rule of
differentiation, there is a corresponding
rule of anti-differentiation, and therefore a corresponding rule of integration.
0.2. Basic Forms. Don’t forget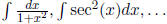 
0.3. u-substitution. From the chain rule. Some tricks: look for du; long
division; complete
the square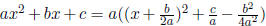 
; to get rid of
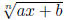, do the substitution
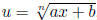, solve for
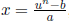, so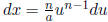 
.
0.4. Powers of trig: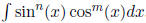 
. The idea: turn
everything into a polynomial
in u = trig function times du. So odd power of sin, pull off one sin, turn
everything into
cos; same for odd power of cos; use sin2(x) + cos2(x) = 1
to convert. (Divide by cos2(x) to
get the sec and tan version, or by sin2(x) to get the csc, cot.) If
they’re both even powers,
use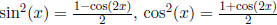 
, or reduction formulas
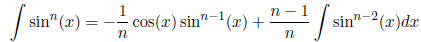
which you derive from parts, u = sinn-1(x), dv = sin(x)dx; likewise
for cos. For powers of
sec, tan, try to pull off sec2(x) and convert to tan(x), or pull off
sec(x) tan(x) and convert
to sec(x). If the powers don’t work out right, you can try to convert to sec and
use
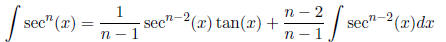
This is again from parts. There’s also a tan formula (derived without parts!)
Finally, these
are difficult (but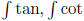 
are not):
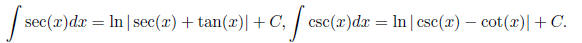
0.5. (Inverse) Trig substitution. Remember
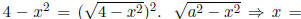
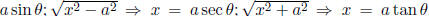. Draw the triangle to get the
radical; back substitute using the triangle or solving for θ; remember
.
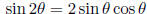0.6. Partial fractions. 1. Long division; 2. Factor denominator; 3. Write
out terms
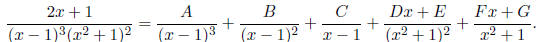
Remember x2 = x×x is a repeated linear factor, not a quadratic. 4.
Solve for A, B, . . . by
equating coefficients or plugging in points. 5. Split and integrate.
0.7. Integration by Parts.
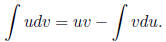
Choosing the right parts is hard – choose u so du is simpler, dv easy to
integrate. If it
doesn’t work try to borrow from the obvious u to dv, and vice versa.