Functions

In this section we examine the following question:

"Is the variable s a function of the variable t?"

The goal of this section is develop a "feel" for functional relationships,
and furthermore, do it in such a way that your understanding
of a functional relationship does not depend on the particular letters
(variables) used. (This is why I have used different letters to denote
the variables - to avoid biasing your thinking towards our special
variables x and y.)

Interpreting the Terminology
In the quotation,

"Is the variable s a function of the variable t?"

the letter s is usually y and the letter t is usually x and so the above
question becomes: "Is y a function of x?". However, it may be that
letter s refers to the letter x and the letter t means letter y, the
question now becomes: "Is x a function of y?" The letters s and t
could represent any pair variables of interest.

Suppose I make the assertion: "s is a function of t." What does this
statement mean, what are its implications?

1. The variable t is to be considered the independent variable.
2. The variable s is to be considered the dependent variable.
3. The acceptable values of the variable t vary over a set of numbers
that is referred to as the domain of the function.
4. The values of the function are symbolically represented by the
letter s. The values of the function come from the range of the
function.
5. There is some rule of association - a rule that associates with
each value of t in the domain of the function, a corresponding
value of s in the range. The rule of association my be given
explicitly or implicitly.
6. Notationally, "s is a function of t" means s = f(t).

Quiz.

1. Consider w as a function of z. Then, corresponding to each value
of z is only one value of w.

(a) True
(b) False

2. Consider h as a function of q. Then h is the independent variable.

(a) True
(b) False

3. Consider x a function of y. Then x may be considered a member
of the domain of the function.

(a) True
(b) False

4. Consider z as a function of x. Then, corresponding to each value
of z is only one value of z.

(a) True
(b) False

5. Consider w as a function of s. Then w may be considered a member
of the range of the function.

(a) True
(b) False

6. Consider t as a function of w. Then symbolically, this means that
t = f(w).

(a) True
(b) False

Passing Score: 6 out of 6.

End Quiz.

Let's now practice recognizing functions through a series of examples
and exercises.

Example 2.14. Let x and y be real-variables. Suppose it is known
that y is related to x by the equation 2x² - 3y = 1.

(a) Is y a function of x?
(b) Is x a function of y?

Exercise 2.41. Suppose x and y are related by the equation 2x -
5y³ = 1.

(a) Is y a function of x?
(b) Is x a function of y?

Exercise 2.42. Let s and t be related to each other by way of the
equation s - 4t + t² = 1.

(a) Is s a function of t?
(b) Is t a function of s?

Exercise 2.43. Consider the equation x² + y + 2 = 1. I wouldn't
think of asking you whether y is a function of x or whether x is a
function of y --- they are not. Let m be any number. Consider the
straight line given by y = mx and visualize the intersection of the line
y = mx with the circle x² + y² = 1.

(a) Is x a function of m, where x is the x-coordinate of the point(s)
of intersection between y = mx and x² + y² = 1.
(b) Let x be the variable described in part (a). Is m a function of
x?

The Vertical Line Test
Suppose you have a curve C drawn in the xy-plane. How can we tell
whether this curve C represents y as a function of x? There is a simple
graphical test.

Important. The x-axis is assumed to be the horizontal axis, and so
the meaning of vertical is perpendicular to the x-axis.

Exercise 2.44. Taking the definition of function into consideration,
the orientation of the axes (x-axis is horizontal), and the geometry of
the graph of a curve, justify in your own mind the Vertical Line Test.

Exercise 2.45. Assume the usual orientation of the xy-axis system
(i.e. the x-axis is horizontal). Suppose we have a curve C in the xy-axis
plane. Under what conditions, similar to the Vertical Line Test,
under which we can assert that the curve defines x as a function of y?

The Vertical and the results of Exercise 2.45 can be consolidated
into a single statement which is stated independently of orientation
of the axis system.

Where, in this test, we do not assume that the x-axis is necessarily
the horizontal axis.

The above concepts are independent of the letters used to describe
them. Here are a couple of questions using other letters.

Exercise 2.46. Let C be a curve in the st-plane. Under what conditions,
similar to the Function Line Test, under which we can assert
that

(a) the curve defines s as a function of t;
(b) the curve defines t as a function of s.

Exercise 2.47. Quiz.

3. Graphing. First Principles

This section still under construction. It is my intention to have a
section here discussing the fundamental principles and techniques
of graphing a function.

4. Methods of Combining Functions

Functions can be combined in a variety of ways to create new functions.
In this section, we discuss ways in which we can use arithmetic
operations for this purpose.

4.1. The Algebra of Functions

Equality of Functions
Let f and g be functions. We say that f = g provided.


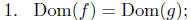
2. f(x) = g(x), for all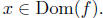

More informally, two functions are the same if they have the same
domain of definition (condition 1), and pointwise they have the same
values (condition 2).

The first example illustrates the equality of two functions. It is a two-step
method: (1) Check whether the domains are equal; (2) Check
whether the functions, pointwise, have the same values.

Example 4.1. Consider the following two functions:

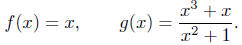
Is it true that f = g?

The next example is almost the same as the previous one, but with
two subtle changes. The signs in the numerator and denominator of
the function g have been changed to negative signs. As in the previous
example, the numerator and denominator have a common factor,
when you cancel the common factor you get g(x) = x, this is the same
definition of f. So the two functions are equal, right?

Example 4.2. Are the following two functions equal?

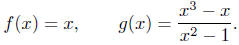
Example 4.3. Consider the following two functions:

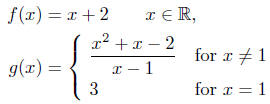
Is it true that f = g?

Exercise 4.1. Determine whether the two functions f and g are
equal.

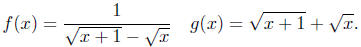
Exercise 4.2. Determine whether the two functions f and g are
equal.

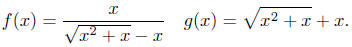
Scalar Multiplication
Let f be a real-valued function of a real variable, and let k ∈ R be a
constant. define a new function, denoted kf, to be a function whose
domain is

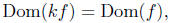
such that,

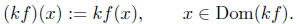
The function kf is called a scalar multiple of f (the constant k, in
this context, is referred to as a scalar).

Below is a sequence of simple examples.

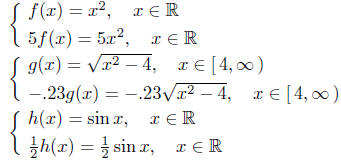
The above discussion covered the construction of a scalar multiple
of a function. A related topic is the recognition of scalar multiples
of functions. For example, consider the function G(x) = 2sinx, you
should recognize (or realize) that his function G is, in fact, a scalar
multiple of a more elementary function, namely the sin function. Thus,
G = 2 sin. (Looks strange doesn't it.)

This ability to recognize scalar multiples is fundamentally a very important
skill.

The Addition/Subtraction of Functions
Let f and g be real-valued functions of a real variable. define f + g
to be a function whose domain is

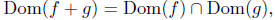
such that

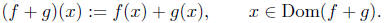
The function is called the sum of f and g. Subtraction of two functions
is defined similarly.

Exercise 4.3. Study the definition of the sum of two functions. Discuss
why the domain of f + g is defined as it is.

Let's look at some illuminating examples.

Example 4.4. Let 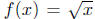and g(x) = sin x, then the sum and
difference of f and g are

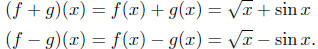
What are the domains of these functions?

Exercise 4.4. Let 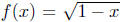and 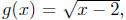and let F =
f + g. Is there something strange about this definition?

The sum and difference of functions is extended to sums and differences
of many functions.

Exercise 4.5. Let f, g, and h be functions. define F = f + g - h.
What is the domain of F, and how do calculate the values of F?

You can combine scalar multiplication and addition/subtraction of
functions.
Example 4.5. Let 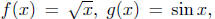and
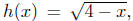
define  F = 2f - 3g + 4h. Discuss the domain of F and obtain a
calculation formula for F.

Recognition. Frankly, a quite a bit more important ability is that of
recognizing sum and differences of functions. For example consider
the function.



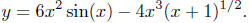
Ideally, when you look at this function, you would, perhaps, in the
natural course of things, make a number of observations: (1) the
function is the difference of two other functions y = 6x² sin(x) and
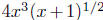; (2) these two functions are scalar multiples of the functions
y = x² sin(x) and 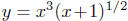. Here, we mentally decompose
the original function 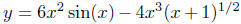into smaller functional
"pieces."

When you look at certain problems in Calculus, for example, this
ability to visually decompose a function this way is fundamental to
correctly analyzing the problem and successfully solving the problem.
(Of course, the functions y = x² sin(x) and 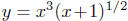can, themselves,
be broken down into smaller functional "pieces;" namely, into
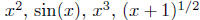- as we shall see in subsequent paragraphs
below.)

Exercise 4.6. Break the function

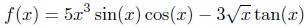
down into more elementary functions.

The Multiplication of Functions
Let f and g be real-valued functions of a real variable. define fg to
be a function whose domain is

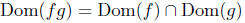
such that,

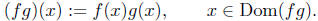
The function is called the product of f and g.

Examples in this section are much the same as in the previous section
on addition and subtraction of functions. Here we have an abbreviated
discussion.

One of the common examples of function multiplication is power functions.
For example, Consider the functions F(x) = x³. Now it may be
convenient to think of F as a "stand-alone" function; Sometimes it
is useful to realize that F is a product of functions, which functions?
Well, define a function f(x) = x, then F(x) = f(x)f(x)f(x), for all
x ∈ Dom(F) = R. This can be written as F(x) = [f(x)]³. Or, if
we want to utilize the concept of equality of functions, we can say:
F = f³. (The f-cubed function, is the function whose value at an
x ∈ Dom(f) is given as [f(x)]³.

Exercise 4.7. In light of the previous discussion, what can be said
about the function F(x) = (2x³-1)⁵ and the function G(x) = sin²(x)?

Now let's get back to a more direct illustration of the product of
functions definition.

Example 4.6. Consider the functions.
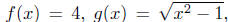
and h(x) = sin(x²). define a new function by F = fgh. Find the
domain of definition of F, and write the calculating formula for F.

Recognition: As in the previous section, it is important to recognize
products of functions.

Example 4.7. Consider the function F(x) = 6x³ sin(x) cos²(x), de-
fine the most basic of functions such that F is the product of them.

Exercise 4.8. Consider the function 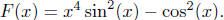If
you wanted to write F in terms of sums, differences, and products,
of "elementary functions," what is the minimum number of distinct
functions needed to do this?

The Quotient of Functions
Let f and g be real-valued functions of a real variable. define f/g to
be a function whose domain is

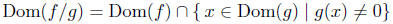
such that,

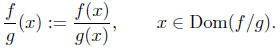
The function is called the quotient of f and g.

Notice the domain of f/g is a bit more involved than the previous
definitions. Obviously, we cannot divide by 0, so we must ensure that
the x we use to evaluate the expression f(x)/g(x), cannot yield 0 in
the denominator; i.e. we require g(x) ≠ 0.

A skill level 0 example would be the following.

Example 4.8. Let f(x) = x³, g(x) = (x² - 1), and define F = f/g.
Discuss the natural domain of definition of F, and write a calculating
formula for F.
Example 4.9. Decompose the function 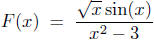into a
products and quotients of "elementary functions." Do a domain analysis
on same.

Comparison of Functions
Comparing functions is quite important in mathematics. It is very
important to understand what is meant by it.

Exercise 4.9. Let f and g be two given functions. Now that you have
seen a large number of definitions, can you give a good definition of
the following phrase:

"f < g over the set A."