- Home
Math 521 Lecture 3 Homework 3
1 Favourites
An arsenal of examples in your head is crucial to processing mathematical
concepts. For each
of the following, list your favourite examples. Make sure your list includes
enough examples to
develop an understanding of the concept. If it is not clear that your example is
an example then
prove that it is.
1. sets
2. functions
3. non-functions
4. relations
5. operations
6. monoids
7. groups
8. rings
9. fields
10. division rings
11. integral domains
12. fields of fractions
13. polynomials
14. formal power series
15. equivalence relations
16. rational numbers
17. irrational numbers
18. algebraic numbers
19. transcendental numbers
20. vector spaces
21. algebras
22. derivations
2 Exercises
1. Let A be a ring and let a ∈ A. Define 0, −a and a-1 and show that 0 ยท a = 0,
0 + 0 = 0,
−(−a) = a, (−1)a = −a, and (a-1)-1 = a.
2. Show that a finite integral domain is a field.
3. Explain how long division works for polynomials and give some examples.
4. Explain why it is necessary to assume that A is an integral domain when
constructing the
field of fractions of A.
5. Show that the addition operation in the field of fractions is well defined.
6. Show that the multiplication operation in the field of fractions is well
defined.
7. Show that the field of fractions is a field.
8. Let A be an integral domain and let F be the field of fractions of F. Show
that the map
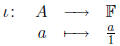
is an injective ring homomorphism.
9. Let A be an integral domain and let F be the field of fractions of F. Show
that if K
is a field with an injective ring homomorphism
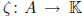then there is a unique
ring
homomorphism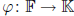 
such that
.
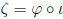10. Let F be a field and let a ∈ F. The evaluation homomorphism
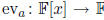F
is defined
from F[x] to F. Discuss thoroughly the issue of extending the evaluation
homomorphism
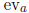to F[[x]], F(x), and F((x)).
11. Let S be a set of cardinality n. Show that
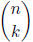is the number of subsets of S of cardinality
k.
12. Show that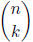is the coefficient of
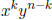in (x + y)n.
13. Show that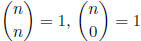 
and, if 1 ≤ k ≤ n − 1, then
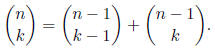
14. Define ex in 6 different ways and prove that all 6
definitions are equivalent.
15. Define ln x in at least 3 different ways and prove that your definitions are
equivalent.
16. Define sin x in at least 3 ways and prove that your definitions match each
other.
17. Explain why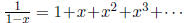 
. What does
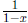mean? Where do these expressions
live?
18. Let n ∈ Z>0. Explain why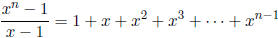 
. What does
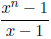
mean? Where do these expressions live.
19. Let n ∈ Z>0. Define
. Prove that
.
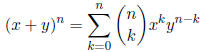20. Define ex and prove that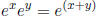 
. Where do these expressions live?
21. Let G = {p(x) ∈ F[[x]] | p(0) = 1}. Show that G is an abelian group under
multiplication.
22. Let g = {p(x) ∈ F[[x]] | p(0) = 0}. Show that g is an abelian group under
addition.
23. Let G = {p(x) ∈ F[[x]] | p(0) = 1} and g = {p(x) ∈ F[[x]] | p(0) = 0}. Show
that
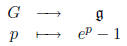
is an isomorphism of groups.
24. Show that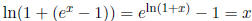 
.
25. Show that there is a unique derivation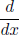 
of F[x] such that 
.
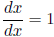26. Show that if p ∈ F[x] then
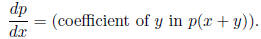
27. Show that if p ∈ F[x] then
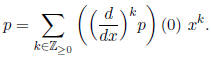
28. Show that there is a unique extension of
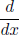to a derivation of F(x).
29. Show that there is a unique extension of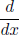
to a derivation of F[[x]].
30. Show that there is a unique extension of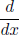
to a derivation of F((x)).
31. Show that if p ∈ F[[x]] then
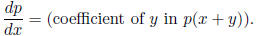
32. Show that if p ∈ F[[x]] then
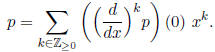
33. Show that if p ∈ F[[x]] then
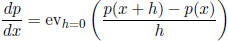
3 Vocabulary
Define the following terms.
1. commutative ring
2. integral domain
3. field of fractions
4. ex
5. ln x
6. sin x
7. cos x
8. derivation