Math Weekly Review

• Monday. Quiz on quotient rule. More on graphing. Product rule for more
than two functions. Derivatives of radicals - part one.

Homework.

1. A function has vertical asymptotes x=1 and x=-3. It passes thru
(0,4). The derivative is negative when x < 0 and positive when
x > 0. Sketch a graph of this function. What can you tell me about
the derivative of the function?

2. Sketch the graph of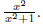
3. p 283 #7
4. p 284 #11
5. p 119 #5
6. p 120 #15
7. p 166 #7 , 18
8. p 155 #23-42 work the ones with a square root.
9. p 155 #47

• Tuesday. Quiz on graphing rational functions. More on the derivative of
radicals and roots - back to the power rule! Composition of functions.
Homework.

1. p 262 #47 (This is like the first few days of class.)
2. p 262 # 51
3. Sketch the graph of f(x) =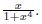
4. Sketch the graph of g(x) =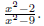
5. p 284 #9
6. Find the maximum and minimum of f(x) = 3x^2 - 12x + 5 on the
interval [0, 3] (0 ≤ x ≤ 3).
7. page 166 #10
8. p 155 #53
9. p155 #58 (a-c)

Wednesday. Graphing quiz? Today we will focus on the chain rule. What
is it and how is it used?

Homework.

1. p 181 #3
2. p 181 #7-10
3. p 210 #5 (Linearization means the best straight line to approximate
the function - what we called the tangent line!)
4. p262 #49
5. Sketch the graph of 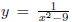Use the derivative and information
about asymptotes, etc.
6. p 284 #10
7. Use the slope/tangent line to approximate 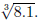Check your answer
by cubing your result. If we did 8.2 instead of 8.1, how would this
change your answer? So, for each increase of x by 0.1, the cube root
of x will increase by (approximately) how much? (Only for x near 8,
of course.)

Thursday. Review of chain rule. Application of tangents. Newton's Method
for (approximately) solving equations { bring your calculators!!!
Homework.

1. p181 #25, 39 (Chain rule review)
2. p181 #43 (Review tangents and chain rule.)
3. p 210 #9 (Review tangents.)
4. p231 # 51 (Review max/min)
5. p 284 #15 (Application. Use the distance formula (see inside, front
cover) and use fact that one point is (0,0) and the other is (x, 4x+7).
Write out the distance and then take derivative. Feel free to use the
calculator to compute derivative.)
6. p 182 #59 (Chain rule - see problem in notes.)
7. Page 298 #1 (Draw a picture with tangents and use to approximate
the roots - using the geometric picture behind Newton's method.)
8. page 298 #5,9 (Do not use the calculator 'tricks' from class. Start
with newroot = x - f(x)/f'(x) and plug in your values.)
9. p298 #13 Now use the calculator tricks from class. Continue iterating
until the solution remains constant in the sixth decimal place. (Place
function into y = menu, for y1. Then at home screen enter a -
f(a)/f'(a)|a = 2. After evaluating replace a = 2 by a = ans.)

Friday. We will review. I have some material and then I plan on breaking
the class into groups and have each group explain a homework problem. Be
prepared to participate - I want to get a better feeling for where everyone
is at before we move on.

Homework. (some may look familiar - I wanted to see if you could do these,
of if you are just not asking questions. I plan to have group presentations
again on Monday.)

1. Sketch the graph of g(x) =
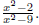
2. Find the point on the graph of y = 1/x+1, that is nearest the point
(5, 5). Start by looking at the graph and making a guess, then set
up an equation and minimize. Be sure that your final answer agrees
(somewhat) with your guess.
3. Use the slope/tangent line to approximate 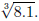Check your answer
by cubing your result. If we did 8.2 instead of 8.1, how would this
change your answer? So, for each increase of x by 0.1, the cube root
of x will increase by (approximately) how much? (Only for x near 8,
of course.)
4. A box with an open top and a rectangular base with length twice the
width must have a volume of 32,000 cubic inches. Find the dimen-
sions of the box to minimize the material used.
5. Sketch the graph of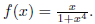
6. Sketch the graph of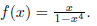
7. Sketch a function f that satisfies all of the following.
f'(2) = 0, f'(0) = 1,f'(x) > 0, if 0 < x < 2,
f'(x) < 0, if x > 2,, as x gets large, f(x) gets very small,
and f(x) = -f(-x).