Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Quadratic Functions: Parabolas

Definitions: Quadratic functions:

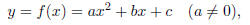
where a, b, c are real numbers.

The Graph of a Quadratic Function

* Shape: parabola, symmetric
When a > 0
When a < 0

* Vertex:

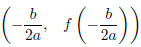
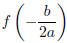is the optimum value (either maximum or minimum) of the function.

* Zeros of quadratic functions = Solutions of the quadratic equation ax² + bx + c = 0

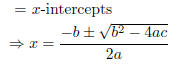
* y-intercept = y value when x = 0

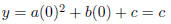
Ex.1 (#6) f(x) = x² + 2x - 3

(a) The vertex
(b) Is the vertex a maximum or minimum point?
(c) x value for the optimal value
(d) The optimal value
(e) Zeros
(f) y-intercept
(g) Graph

Ex.2 (# 36) If 100 feet of fence is used to enclose a rectangular yard, determine the length and width of
the rectangle that give maximum area.

Shifting Graphs

Compare vertices.

Ex.3 How is the graph of y = x² shifted to get the graph of

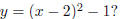
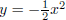Ex.4 How is the graph of shifted to get the graph of

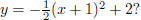
Average Rate of Change

The rate of change of a quadratic function is not constant.

-> use the average rate of change between two points.

Definition: The average rate of change of f(x) between two points x = a and x = b (a < b) is

Average rate of change

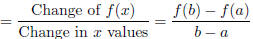
= Slope of the line between (a, f(a)) and (b, f(b))

Ex.5 (#42) The figure (on p.160) shows the graph of a total revenue function, with x equal to the
number of units sold.

(a) Is the average rate of change of revenue negative from x = a to x = b or from x = b to x = c?
Explain.

(b) Would the number of units d need to satisfy d < b or d > b for the average rate of change of
revenue from x = a to x = d to be greater than that from x = a to x = b? Explain.

Home