Joys and virtues of obsolete technologies

Obsolete

Definition:
1 No longer produced; out of date.
2 Biology Less developed (formly or related species);
rudimentary; vestigial.
• I just bought a computer and now it is obsolete.
• The dinosaurs disappeared from the historical record.
• This antique is valuable because they stopped making
them.
• Vestigial organs like the appendix.
Steven

Which is larger?

Which of e^x or π^e is larger?

Found as the problem of math riddles book in the 1960’s
Perhaps a Math Puzzle book by Martin Gardner
Perhaps The Unexpected Hanging and Other Mathematical
Diversions 1969.

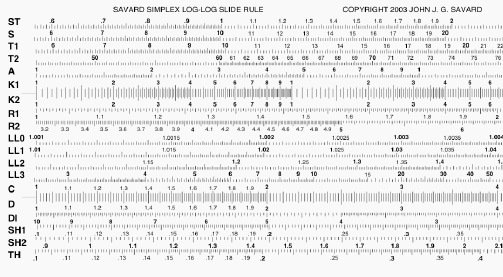
Log-Log Duplex Deci-Trig
 

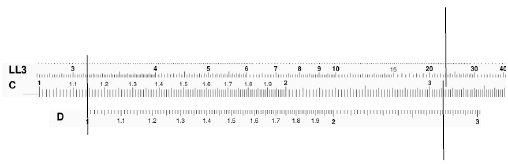
Slide Rule

• invented by Oughtred in 1622 just a few years after
logarithms.
• Mannheim (1851) Modern slide rule with A, B, C and D
scales.
• Made the trip to the moon with Apollo.
• essentially disappeared in 1970’s when all the slide rule
manufactors silently quit, perhaps in response to the HP
35.
• now a collectors item.
• variations in size, circular, with microscope.
• Over 40 million produced.

Virtues of the Slide Rule

• Scientific notation, estimation, no batteries required.
• Develops analog reading abilities. (Gauges, dials)
• Parallel computing.
• Wonderfull applicaton of Logs. Intermediate value
theorem.
• Intermediate results were stored.
• Stable design:

Slide Rule Scales

• Napier’s Bones 1617
• Doubled the life of astronomers.
• Great application of the laws of exponents.
• Linear interpolation
• Table lookup also used for trig, factors, integrals, Laplace
transforms . . .
• Which is larger log log π + log e or log log e + log π ?

Math Wars

Math wars was roughly speaking a term used over the battle
over pencil and paper calculation vs calculators.
• Which was the correct way to introduce elementary age
children to arithmetic. (US education 1990’s)
• Which is the correct way to do arithmetic. (Algorists vs
Abacists, the 400 years war)

400 Years War

From roughly 1100 to 1500 there was a battle between:

Abacists Use Roman numerals along with the abacus.
Algorists Use Hindu-Arabic numerals along with the appropiate
algorithms for calculation.

Highlight: Florence 1299 forbid the use of the new numbers in
financial procedures.

Roman Numerals

• Letter stand for values: I for 1, V for 5, X for 10, L for 50, C
for 100, D for 500, M for 1000.
• Arranged in decreasing size. (MCV and not CVM)
• Letters are repeated for missing values: III for 3, XX for 20,
etc
• Sometimes shorthands: IV for 4, CM for 900.
• Other extensions.

Virtues of Roman Numerals

• Forced one to use an abacus (matched too)
• Much harder to alter entries (try changing an id’s XVIII to
XXI)
• numeral vs number
• Look important? Use on clocks and movie copyright dates.

Virtues of Abacus

• Counting table ancestor: some lines in the sand and some
stones to count with. Indeed calculate comes from calculus
which is latin for stone. Abacus comes from the greek
abax, table covered with sand or fine dust
• positional representation. (1950’s netherlands used them
in education)
• paperless office (paper wasn’t cheap in dark ages)
• add, subtract, multiply, divide

There is a on-line book on how to use the abacus

Euler turns 300

Euler didn’t have the technology to prove his analytical results
with the same rigor required by today’s standards. Or he lived
before Cauchy invented 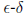technology.

• The Basel problem 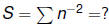was first done
numerically.
• Euler knew π= 3.141592653589793238 . . .
• Euler computed S = 1.6449340668482264364 . . .
• Euler came up with an agruement that S = π^2/6 and the
numbers above proved it. (It is better than the current
experiments of quantum mechanics)
• Euler eventually answered all the weaknesses of his
agruement, — some many years later.

Summing ζ(2)

• Integral test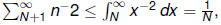 Euler needed to
sum 10¹⁹ terms.
• The Euler-MacClaurin formula.
• Accelerating series convergence, Euler transformation
x = y/(1 − y) maps y = 1/2 to x = 1.
• Is this like turing completeness? Namely the fastest
computer can’t do anything a turing machine can do, nor
any faster mod polynomial time.

Divergent Series

Abel on divergent series (1828):
. . . Divergent series are in general the work of the devil and it is
shameful to base any demonstration whatever on them . . . For
the most part the results are valid, it is true, but it is a curious
thing. I am looking for a reason and it is a very interesting
problem.
Modern theory starts with Frobenius(1880).A good source is
Hardy’s book (1948) [Now printed by AMS (1992).]

Human Calculators – Idiot Savant Dase

A person who is mentally handicapped (or otherwise is
ordinary) but displays brilliance in one area, especially one
involving memory.
• Computed π to 200 digits
• Hired by Gauss (first person to buy computer time?) to
factor the intergers from X to Y.

Human Calculators – WW2

Calculator was a job title during World War II. Often female, she
would do calculations for the military.

Slide Rule in High School Education circa 1964

• Taught in Chemistry class. Along with scientific notation,
the ideal gas laws and molarity calculations.
• Getting the decimal point correct. (Estimation.)
• Percentage error, significant digits.
• Low cost items, roughly $3 ($15-$20 in current money)
• No S or T scales, so the technology wasn’t used in
Trigonometry class. (Most Trig students had already taken
Chemistry.) Trigonometry classes used tables of trig and
log functions.
• Drawing and reading graphs.

Success of the Calculus Reform

The rule of four:
• Graphs to replace reading scales (gauges)
• (Numerically) Tables to replace using log/trig tables
• Verbally to replace what?
• Formulas to replace what?

Programing Assignment #7

Wag the dog

• Graphics Processors double in speed every 12 months (vs
18 for CPUs).
• But they are for games, hence only single percision.
• Slide rules disappeared because they were a small and not
very profitable part of scientific instruments.
• HP quit making graphing calculators briefly. The TI-89
hasn’t improved mathematically since 1999 and the price
as gone up.

Victorian Internet

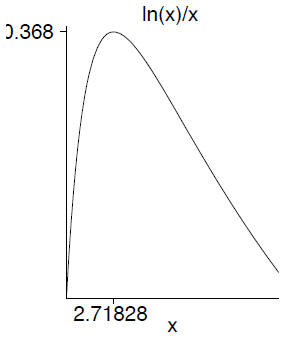
Larger – revisited

Need to maximize 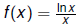which by calculus happens when
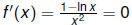or ln x = 1 or x = e So a^e < e^a for all a ≠ e
including π.

e^π Wins

• Does the history of obsolete technology give insight into
the rapid change of today’s techonology?
• The analog world had virtues.