SOLUTIONS TO MATH MIDTERM II
1. Find the arclength of the curve y = ex from
x = 0 to x = 1.
Since y is a function of x here, we can represent the arclength of the curve in
terms of an integral with respect to x, i.e,
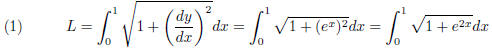
To evaluate the integral, we need to make a substitution:
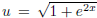 . then
. then
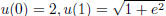 . To write integral with respect to u, we
need to write dx
. To write integral with respect to u, we
need to write dx
in terms of u. From the substitution, it follows e2x = u2
− 1, hence by taking ln at
both sides

then
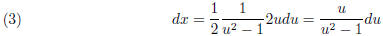
The integral becomes
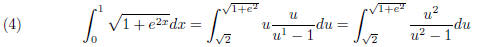
in which the integrand is a rational function. It is not a
proper rational function,
we need to do long division to apply the partial fractions. The long division
here
is very simple: u2 = (u2 − 1) * 1 + 1. hence
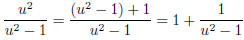
It follows (note u2 − 1 = (u + 1)(u − 1))
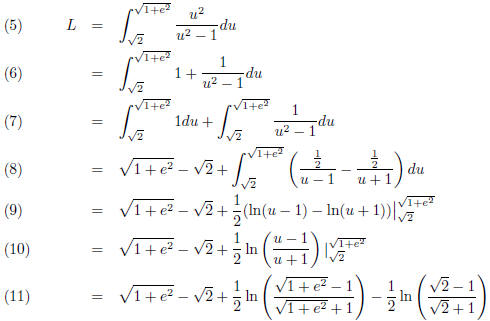
2. Find the solution to the initial value problem
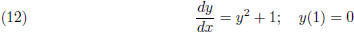
The RHS of the equation is a function of y.hence by
seperating the variable we
get

Integrating both sides
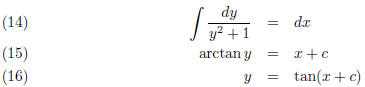
The initial condition y(1) = 0 yields

Hence c = kπ − 1 where k is an integer. Hence the
solution to the initial value
problem is

Since tan(x + kπ − 1) = tan(x − 1) holds for any x.
the solution to the I.V.P.
becomes

3.Find the slope of the tangent line to the curve

at the point corresponding to t = 1.
As we know, the slope m at one point is defined to be
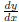 at that point. i.e,
at that point. i.e,

On the other hand
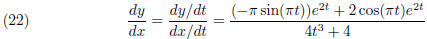
When t = 1
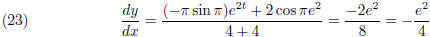
Hence the slope at the given point is
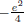 .
.
4. Consider the point with the Cartesian coordinates
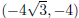 . Find the
. Find the
polar coordinates (r, θ) of the point, where r > 0 and 0 ≤ θ < 2π
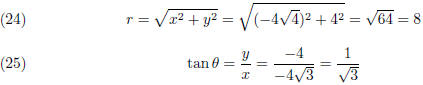
we know
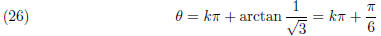
where k is an integer. On the other hand, it is obvious
the point is in the third
quadrant (Please plot the point and you will see it) . Hence

since r > 0. ( What if r < 0?) It follows k = 1, i.e,

Hence the required polar coordinates for the point are
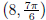
5. Identify the curve by finding the cartesian equation for the curve

Multiply both sides by r gives

Now since
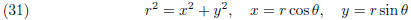
It follows
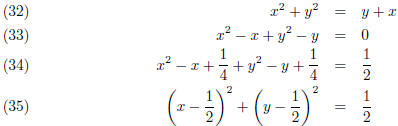
Hence the curve is a circle with center
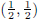 and radius
and radius
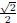 .
.




