The Integers and Division

Of course, you already know what the
integers are, and what division is…

But: There are some specific notations,
terminology, and theorems associated with
these concepts which you may not know.

These form the basics of number theory.

Vital in many important algorithms today
(hash functions, cryptography, digital
signatures).

Divides, Factor, Multiple

Let a, b∈Z with a≠0.

Def .:a|b≡“a divides b”:≡( c∈Z:b=ac)
“There is an integer c such that c times a
equals b.”

Example: 3|12 True, but 3|7 False.

Iff a divides b, then we say a is a factor or a
divisor of b, and b is a multiple of a.

Ex.: “bis even”:≡2|b.

Facts re: the Divides Relation

Theorem: a,b,c ∈Z:



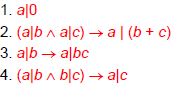
Proof of (2): a|b means there is an s such
that b=as, and a|c means that there is a t such
that c=at, so b+c= as+at= a(s+t), so a|(b+c)

More Detailed Version of Proof

Show .

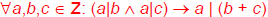Let a, b, c be any integers such that a|b
and a|c, and show that a| (b+ c).

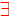By defn. of |, we know s: b=as, and
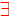t: c=at. Let s, t, be such integers.

Then b+c = as+at= a(s+t), so
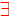u: b+c=au, namely u=s+t. Thus a|(b+c).

Prime Numbers

An integer p>1is prime iff it is not the
product of two integers greater than 1:



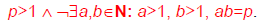
The only positive factors of a prime pare 1
and p itself. Some primes: 2,3,5,7,11,13...

Non-prime integers greater than 1 are
called composite, because they can be
composed by multiplying two integers
greater than 1.

Fundamental Theorem of Arithmetic

Its "Prime Factorization"

Every positive integer a unique
representation as the product of a non-
decreasing series of zero or more primes.

Some examples:
1 = (product of empty series) = 1
2 = 2 (product of series with one element 2)
4 = 2·2 (product of series 2,2)
2000 = 2·2·2·2·5·5·5; 2001 = 3·23·29;
2002 = 2·7·11·13; 2003 = 2003(no clear pattern!)

An Application of Primes!

When you visit a secure web site (https:…address,
indicated by padlock icon in IE), the browser and web
site may be using a technology called RSA encryption.

This public-key cryptography scheme involves
exchanging public keys containing the product pq of two
random large primes p and q (a private key) which must
be kept secret by a given party.

So, the security of your day-to-day web transactions
depends critically on the fact that all known factoring
algorithms are intractable!

Note: There is a tractable quantum algorithm for
factoring; so if we can ever build big quantum
computers, then RSA is not secure.

The Division “Algorithm”

It’s really just a theorem, not an algorithm…

Only called an “algorithm”for historical reasons.

Theorem: For any integer dividend a and
divisor d≠0, there is a unique integer
quotient q and remainder r∈N such that a =
dq+ r and 0 ≤r < |d|. Formally, the theorem
is:



We can find q and r by: .

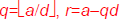Greatest Common Divisor

The greatest common divisor gcd(a,b) of
integers a, b (not both 0) is the largest (most
positive) integer d that is a divisor both of a
and of b.



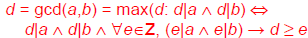
Example:gcd(24,36)=?
Positive common divisors: 1,2,3,4,6,12.
The largest one of these is 12.

GCD shortcut

If the prime factorizations are written as
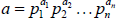and ,
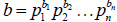then the GCD is given by:

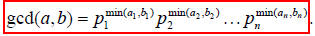
Example of using the shortcut:

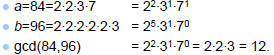
Relative Primality

Integers a and bare called relatively
prime or coprime iff their gcd= 1.

Example: Neither 21 nor 10 is prime, but
they are coprime. 21=3·7and 10=2·5, so
they have no common factors > 1, so their
gcd= 1.

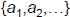A set of integers is (pairwise)
relatively prime if all pairs 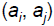, for i≠j,
are relatively prime.

Least Common Multiple

lcm(a,b) of positive integers a, b, is the
smallest positive integer that is a multiple both
of a and of b. E.g.lcm(6,10)=30



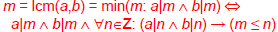
If the prime factorizations are written as
and

then the LCM is given by

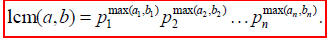
The mod operator

An integer “division remainder” operator.

Let a,d∈Z with d>1. Then a mod d
denotes the remainder r from the division
“algorithm”with dividend a and divisor d;
i.e. the remainder when a is divided by d.

Using e.g. long division.

We can compute (a mod d) by:



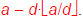
In C/C++/Java languages, “%”= mod

Modular Congruence

Let a, b∈Z, m∈.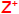
Where 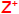={n∈Z| n>0}=N−{0}(the + integers).

Then a is congruent to b modulo m,
written “a≡b(mod m)”, iff m | a−b.

Note: this is a different use of “≡”than the
meaning “is defined as” I’ve used before.

It’s also equivalent to: (a−b) mod m = 0.

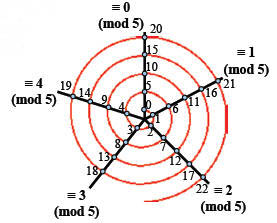
Spiral Visualization of mod≡

Example shown:
modulo-5
arithmetic

Useful Congruence Theorems

Theorem: Let a,b∈Z, m∈. Then:


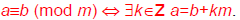
Theorem: Let a,b,c,d∈Z, m∈. Then if
a≡b(mod m) and c≡d(mod m), then:
▪a+c≡b+d(mod m), and
▪ac ≡bd(mod m)