Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Reading Questions for Section 5.5

1. Work through Example 1 of Section 5.5 by graphing both f (x) = x² and g(x) = −2(x +1)² + 3 on
your grapher in an appropriate viewing window. Knowing what you do from Sections 5.1-5.3,
complete the blanks, choosing from the set of words {up, down, left, right}. The graph of g(x) is
obtained from the function f(x) by shifting the graph of f(x) ________ 1 unit, followed by
stretching it vertically by 2, followed by shifting it ______ 3 units.

2. Write the function g(x) in Example 1 of Section 5.5 in standard form: g(x) =_______________

3. The standard form for a quadratic function makes it easy to identify the vertical (or y-) intercept.
o True
o False

4. What is the vertical intercept of the function g(x) in Example 1 of Section 5.5? ( ____, ____ )

5. If a < 0, then the graph of the parabola, y = −ax² opens
o downward
o upward
o to the left
o to the right

6. Which of these forms for a quadratic function make it easiest to identify the zeros?
o standard form
o vertex form
o x-intercept form
o factored form
o none of these

7. How does the text convert a quadratic function from vertex form to standard form?
o by completing the square
o by performing a series of shift transformations and either a vertical stretch or a vertical compression
o by multiplying out the squared term and combining like terms
o by applying the quadratic formula or factoring the expression

8. How does the text convert a quadratic function from standard form to vertex form?
o by completing the square
o by performing a series of shift transformations and either a vertical stretch or a vertical compression
o by multiplying out the squared term and combining like terms
o by applying the quadratic formula or factoring the expression

9. Convert the formula for the parabola in Example 4 to standard form:

10. Convert the formula for the parabola in Example 4 to vertex form:

11. Match the following quadratic functions to their vertex point.

____ f(x) = x² − 1	A. (0, 1)
____ u(x) = x² + 1	B. (1, 0)
____ v(x) = (x + 1) ²	C. (0,−1)
____ w(x) = (x − 1)²	D. (−1, 0)

12. If y = x² + bx + c then to complete the square you add and subtract which one of the following values?
o b/2
o b/c
o (b/2)²
o
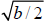
o None of these

Home