Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

MATRIX ALGEBRA

Example: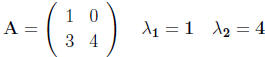

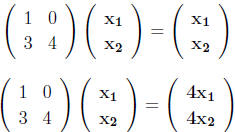
From the first expression,

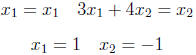
From the second expression

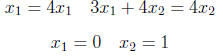
Usual practise to determine an eigenvector with length one. In the example:

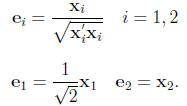
Definition: Quadratic form Q(x) in k variables , where ,
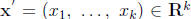is defined as

Q(x) = x'Ax where A is a fix (k × k) matrix

The quadratic form is a quadratic function of .

Example:

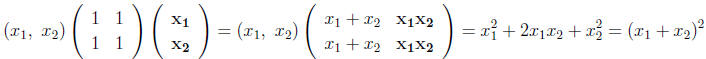
Theorem Let A be a (k × k) symmetric matrix, (i. e. A = A') then A has k pairs of
eigenvalues and eigenvectors

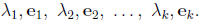
The eigenvectors can be chosen to satisfy

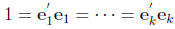
and be mutually perpendicular. The eigenvectors are unique unless two or more eigenvalues
are equal.

Definition: Positive Definite Matrices Let A be a symmetric matrix (k × k). A is
said to be positive definite if
x'Ax > 0 for all x ∈ R^k x ≠ 0.

A is positive semi-definite if
x'Ax ≥ 0 for all x ∈ R^k.

Theorem: Spectral decomposition of a symmetric (k × k) matrix A is given:

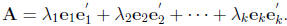
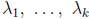are eigenvalues of A and 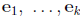are the associated normalized eigenvectors.

Theorem A, (k × k) symmetric matrix is positive definite if and only if every eigenvalue
of A is positive.

A is positive semi-definite if and only if every eigenvalue of A is nonnegative.

Proof: Trivial from the spectral decomposition theorem.

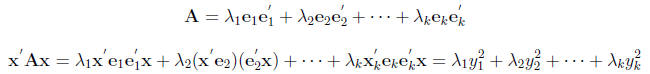
where 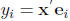. Choosing x = , j = 1, . . . , k) follows the theorem.

Another form of the spectral decomposition:

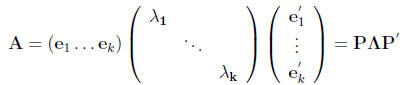
INVERZE AND SQUARE ROOT OF A POSITIVE DEFINIT MATRIX
By the spectral decomposition, if A is positive definite:

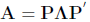
Inverse of A If A is positive definite, then the eigenvaluse of A are
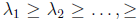
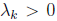i = 1, . . . , k. The inverse of A is 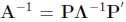where .

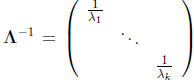Because;

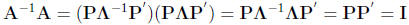
Square Root Matrix (defined for positive semi-definite A)

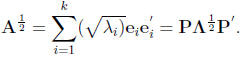
Notice:

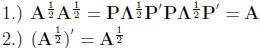
MATRIX INEQUALITIES AND MAXIMIZATION

Cauchy-Schwarz Inequality: Let b, d ∈ R^p, then

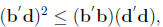
with equality if and only if b = cd.

Proof: The inequality is obvious when one of the vectors is the zero one. For b − xd ≠ 0 we
have that,

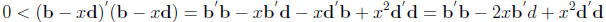
Adding and substratcting 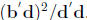, we have that

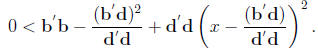
Choosing x = b'd/d'd follows the statement.

Extended Cauchy–Schwartz Inequality: Let b, d ∈ R^p and let B be a positive definite
(p × p) matrix. Then

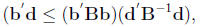
with equality if and only if b = cB^-1d for some constant c.

Maximization of Quadratic forms on the Unit Sphere:

Let B be a (p × p) positive definite matrix with eigenvectors 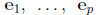and associated
eigenvalues 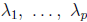eigenvectors, where . Then

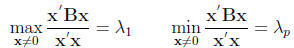
Moreover

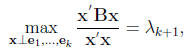
and the equality is attained when .

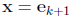Home