- Home
Practice Final Exam, Solutions
Below are the solutions to all problems contained on the
Practice Final Exam. Keep in mind that the
solutions I give below are very complete and thorough, and that I’ve provided
them for study purposes;
I would not expect most of your answers on an exam to be as thorough or
well-worded as mine below!
If you have any questions about these solutions (or if you think you’ve found a
typo!), please let me
know.
1. (16 points total; 4 points each) Indicate whether each
statement is true or false, and provide a
one-sentence explanation for your answer.
(a) The domain of the function sec(x) is (-∞,∞).
This is false: recall that sec( θ ) = 1
cos( θ ) , so sec( θ ) will be undefined whenever cos( θ ) = 0.
This occurs when
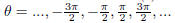(that is, at all numbers
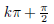for integers k). In
particular, it occurs, which means there are places, listed above, where the
function sec( θ ) is
undefined.
(b) Every real number is a rational number.
This too is false: there are numbers that are not rational. (That is, they
cannot be written as
fractions, p/q , where p and q are integers, q ≠ 0.) For instance π, e, and
sqrt(2) are all irrational.
(c) The Vertical Line Test can be used to tell whether a function is one-to-one
or not.
This too is false: the VLT allows us to see whether or not a graph is the graph
of a function
in the first place. The Horizontal Line Test allows us to tell whether a
function is one-to-one
or not.
(d) The leading coefficient of a polynomial of the form p(x) = a0 + a1x + · · ·
+ anxn is a0.
Wow, another false statement!: the leading coefficient is the coefficient on the
highest power
of x. In the example above, this coefficient is an.
2. (32 points total; 8 points each) Solve each of the following equalities.
(a) |2x + 5| − 3 = 0
First, move the 3 to the other side, obtaining |2x + 5| = 3. Recall that there
are now two
possibilities for 2x+5; either 2x+5 = 3 or 2x+5 = −3. In the first case, 2x = −2
=> x = −1;
in the second case, 2x = −8 => x = −4. Thus we obtain the solutions x = −1 and x
= −4.
(b)
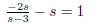
Let’s bring everything over to one side of the equation and find a common denominator:
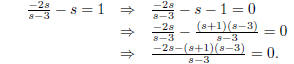
Recall that a fraction is 0 only if its numerator is 0
(and its denominator is not). Thus we
solve:
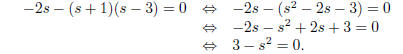
This is now easily solved: 3 = s2 => s = ±sqrt(3). Since neither of these values for s makes the
denominator s − 3 equal to 0, these are our solutions: s = ±sqrt(3).
(c)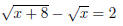
We need to get rid of the radicals, and the best way to do
that is to square the equation, but
first we do a little rearrangement:
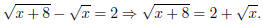
Now square both sides, obtaining
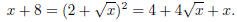
This is now easily solved by canceling terms on both
sides, to obtain 4sqrt(x) = 4, or
sqrt(x) = 1.Squaring once more, we find our only solution, x = 1.
Recall that we have to check to make sure this isn’t a “false” solution (which
could arise from squaring in the first place!):
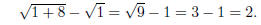
Thus we really do have a solution, x = 1.
(d) tan( θ ) = 0
Recall that tan( θ ) = sin( θ )/cos( θ ) . This fraction will only equal 0 when the numerator equals 0; that
is, when sin( θ ) = 0. As we saw in class, this happens when the y-coordinate of
our point on
the unit circle is 0, which occurs at the following values of θ :
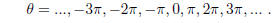
That is, tan( θ ) = 0 if and only if θ = kπ for some integer k.
3. (27 points total; 9 points each) Let f(x) =sqrt(x − 19), g(x) = x^3 − 8, and h(x) = ln(x).
(a) Find the domain of each of the functions f, g, and h.
Since we can’t take the square root of a negative number, for f we require that
x−19 ≥ 0, or
x ≥19. Thus the domain of f is [19,∞).
Since we can plug any number into any polynomial, the domain of the polynomial g
is
(−∞,∞).
Finally, we cannot take the logarithm of a number less than or equal to 0. (One
way to
remember this is to remember that the log ln(x) gives the power of e needed to
obtain the
value x; if x ≤ 0, no power of e will equal it!) Thus the domain of h is (0,∞).
(b) Find a formula for the composition h ο g, and give the
domain of this function.
The composition is easily computed:
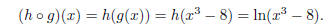
For this function to be defined, we need that g is defined
at x and that h is defined at g(x).
Since g is defined everywhere, the first condition is met. Referring to our work
in part (a),
the second condition requires x3 − 8 > 0. This is easily solved:
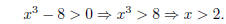
Thus the domain of h g is (2,∞).
c) Find a formula for the composition f g, and give the
domain of this function.
The composition is easily computed
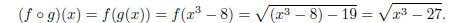
As before, any old x can be plugged into g, but we also
need that x3 − 27 ≥ 0, which gives
x3 ≥ 27, or x ≥ 3. Thus the domain of f g is [3,∞).
4. (15 points total) Let f(x) = 3(ex-1) + 5.
(a) (7 points) Use shifting and stretching of basic
functions to sketch a graph of the function
f. (Be sure to provide a scale for your axes, and indicate at least one point on
the graph
precisely.)
Your graph should begin with the graph of the function ex and then
i. shift this graph to the right by 1 unit, then
ii. stretch the graph vertically by a factor of 3, and finally
iii. shift the graph up by 5 units.
As a point of reference you could indicate that the point (0, 1) on the original
graph goes to
(1, 1), then (1, 3), then (1, 8) under the process above. Note also that the
horizontal asymptote
y = 0 of the function ex will give a new asymptote, y = 5, for our function f.
(b) (8 points) Find the inverse to the function f, writing
it as y = f-1(x).
We write y = 3(ex-1) + 5 and solve for x in terms of y:
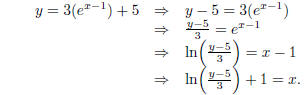
Now all we have to do is switch the roles of x and y:
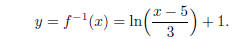
5. (32 points total; 8 points each) Let
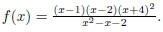
(a) Find the domain of the function f.
The only problem we might encounter is dividing by 0. Thus we must exclude those
x that
make the denominator 0. To find these xs, we factor the denominator:
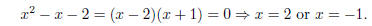
Excluding these two points gives us the domain
.
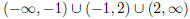Incidentally, notice that if x ≠ 2 we can cancel that term from the numerator
and denominator,
obtaining the simpler function
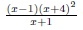which equals f(x) except when x = 2.
(b) Find all zeroes of the function f.
The zeroes (also known as roots) of the function are those values of x at which
the function is
defined and equal to 0. Since rational functions are equal to 0 if and only if
their numerators
are equal to 0, we note
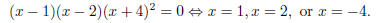
Since x = 2 is not in the domain, this value does not give
a zero, and we have zeroes at x = −4
and x = 1.
Incidentally, we could have considered the simplified function
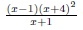and gotten the same
zeroes! In either case, the value x = 2 will give a hole in the graph.
(c) Find all asymptotes of the function f.
Now we consider the simplified function
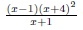, having already decided that there’s a
hole in our graph at x = 2.
Since the denominator is 0 at x = −1, we know that we will have a vertical
asymptote at
x = −1.
To find horizontal asymptotes (if any), we examine what happens for BIG values
of x:
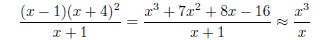
for such values of x, since the leading terms of the
numerator and denominator are the terms
that dominate. But x3/x = x2. Since this is not a constant value, there is no line y = constant
that our function approaches. Therefore there is no horizontal asymptote.
(Rather, in the
long run the function behaves a lot like a parabola, and you can make use of
that information
in part (d) below!)
(d) Use the information from (a), (b), and (c) to sketch a
graph of the function f. (Be sure that
your graph is consistent with the information from the first three parts!)
Just make sure that you incorporate the information above regarding the hole at
x = 2, the
asymptote at x = −1, the zeroes at x = −4 and x = 1, and the long-term parabolic
behavior
we determined in (c). Beyond this, maybe evaluating f at a few other points
(like f(0) = −16,
f(3) = 24.5, and so forth) could help you sketch the graph.
6. (30 points total; 10 points each) Give brief definitions or explanations of
the following concepts;
you may use examples or diagrams if appropriate. The clearer, more complete, and
more correct
your answer, the better.
(a) Horizontal Line Test
The HLT tells us that a function f is one-to-one if and only if any horizontal
line intersects
the graph of f in at most one place. The test works because if a line intersects
the graph at
two different places, say at x = x1 and x = x2, then f(x1) = f(x2), violating
the condition
that we’d need for f to be one-to-one.
(b) function
Put simply, a function f with domain A and range B is a rule that assigns to
every element of
the set A a unique element in the set B. The keys here are the words “every” and
“unique”:
we have a function if and only if every element in A gets assigned something in
B, and this
assigned element is unique.
(c) secant line (to the graph of a function)
A secant line to the graph of the function f is any line that intersects the
graph in two points,
(x1, f(x1)) and (x2, f(x2)). The slope of this line can be used to estimate the
slope of the
function’s graph, by taking the points x1 and x2 to be quite close together.
7. (10 points) Rationalize the numerator in the expression
.
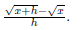To perform this operation we have to use the conjugate of the numerator,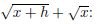
:
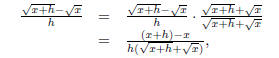
where the final numerator comes from simplifying the
product of the previous numerators. But
now we can simplify a touch more and obtain our final expression:
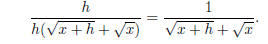
Note that the denominator must now unavoidably contain
that nasty conjugate expression; there’s
no way around that! However, for certain applications, this is all right.
8. (20 points total) Let
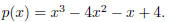
(a) (8 points) Find all roots of the function p.
Using the Rational Root Theorem, our only possible roots are of the form ±1, ±2,
or ±4.
(You should review this theorem briefly if you don’t remember what it says!) To
find our first
root, we just try each of these values in turn. Happily, the first one, x = 1,
is in fact a root.
We can then long divide x3 −4x2 −x+4 by x−1 and obtain the quotient x2 −3x−4,
which
is easily factored as (x − 4)(x + 1) using the AC Method or just by inspection.
Thus we have
the roots x = −1, x = 1, and x = 4.
(b) (6 points) What happens to the value of p(x) as x approaches ∞? As x approaches −∞?
As x approaches ∞, the term that dominates in p(x) is the leading term, x3.
Since the leading
coefficient, 1, is positive, the function p(x) will behave like x3 and grow
without bound and
become increasingly large, positively, for large values of x.
Similarly, as x approaches −∞, the function behaves like x3 and grow arbitrarily
large, negatively.
(c) (6 points) Use the information in (a) and (b) to sketch a graph of the function p.
The information above should help you draw a graph that passes through the
x-axis at the
values x = −1, x = 1, and x = 4, and that grows positively in the direction of 1
and
negatively in the direction of −∞.
9. (18 points total; 6 points each) Simplify each expression as much as possible
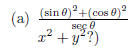(Hint: if the point (x,
y) lies on the unit circle, what can you say about
x2 + y2?)
Recall that the sine and cosine of an angle represent, respectively, the y- and
x-coordinates
of a point on the unit circle. Thus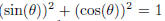 
for any
Our expression then
reduces easily, remembering that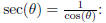 
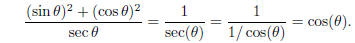
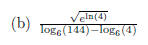
The top simplifies by canceling the inverse functions ex
and ln(x) with one another: eln(4) = 4.
Thus the top is sqrt(4) = 2.
The bottom simplifies by recalling that “the difference of logs is the log of
the quotient”:
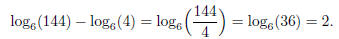
Thus the whole expression is 2/2 = 1.
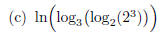
Keep your cool! Just do one log after another, working from the inside out:
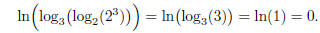
Extra Credit. (5 points) Come up with a mnemonic phrase
for remembering the quadrants in which the various
trigonometric functions are positive.
Of course, the standard one is “All Students Take Calculus,” but I hope you can
let your imaginations
run wild!