Rationals number

Recall that we just proved a theorem which says that for any interval of the
real numbers, (a, b) there exists a rational number q such that a < q < b: If
there is one, can we show there is 2? Sure, consider the new interval (q, b)
and use the theorem again. In fact, it seems like we could continue doing
this over and over again to get an infinite number of rationals in the interval.
Lets prove this is true but instead of inductively generating an infinite set
this way, lets prove it by using a contradction.

That is, we will assume there is a finite number of rationals in the interval.
We will then create a new rational number in the interval by taking two
rationals in the interval and averaging them to get a new rational between
them.

1. Prove there are an in nite number of rationals in any interval
(a,b)

Suppose there are a nite number of rational numbers in the interval, call
this set A

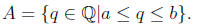
Recall from the discussion above that we have at least two rationals in this
interval so this set has at least two members. Since this set is finite and has
at least two elements, we can choose two of its elements with out another
element in between them. For example, we could pick the two largest elements.
Lets call these m and n. But then, (m+n)/2 is also a rational number and

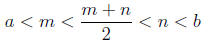
so, 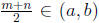and between m and n so we get a new rational not in our
original set A. This is a contradiction to our assumption that A had all of
the rationals between a and b in it. Hence, the set must be in finite.

2. Prove using mathematical induction that 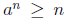for all

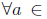
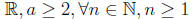
We will prove this for an arbitrary a by using mathematical induction on n.

Base case We begin with the base case, n = 1
For this case we have a¹2¹ 1 so the base case checks.

Induction step: P(n) -> P(n+1)

We assume P(n) is true and use this to prove P(n+1).
That is, assume aⁿ≥n for all a≥2:
Then, consider aⁿ⁺¹ = aⁿa: We can now use P(n) to substitute in for aⁿ. We
thus obtain,

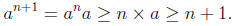
We see that the last inequality is true because, since n≥1,

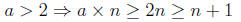
Hence, we have shown P(1) is true and P(n) -> P(n + 1) is true. So, by the
Principle of Mathematical Induction, we know that P(n) is true

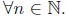
3. Let S be a set of real numbers, and x be a real number. Show
that x = sup(S) iff

a .) x is an upperbound of S, and

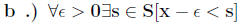
Since this statement is of the form P <-> Q we will first prove P -> Q
then Q -> P. First, we recall the definition of x = sup(S) requires that

1 .) x is an upperbound of S, and
2 .) for every upperbound x' of S, x≤x'

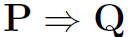
That is, I will assume that x = sup(S) and show a.) and b.).

a.) is immediate from the definition of sup. That is x = sup(S) -> x is an
upperbound of of S by definition.

For part b.) we want to show that for any 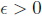we can find an element of S
greater than x-e: Since x is the least upperbound and 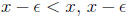can
not be an upperbound of S. That is, there must be an element of S which is

greater than 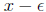and so b.) must be true.

Hence, we have shown P -> Q now we must prove the other direction.

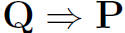
This direction is very similar to the other one. We are going to assume a.)
and b.) and prove that x = sup(s).

First, requirement a.) is exactly the same as 1.) so we are half way there
since we assumed a.

Next, we attempt to prove 2.) from b.) . That is, we want to show that if
b.) is true we know that x must be the least upperbound.

Lets prove this by contraction, that is, lets assume b.) is true and x is not
the least upperbound. So, there is another upperbound x' which is strictly
less than x. But then, set

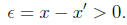
Then, b.) tells me that there must be an element s ∈S for which

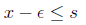
Recall,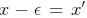 which was assumed to be an upperbound so we have a
contradiction since there is an element of S which is greater than x' so it
can't be an upperbound.

Hence, we have proven a:)&b:) -> x = sup(S):

Finally, we have proven both a:)&b:) -> x = sup(S) and x = sup(S) ->
a:)&b:) so we have a:)&b:) <-> x = sup(S):