Math 18.06 Exam 1 Practice

General comments

Exam 1 covers the first 8 lectures of 18.06:

1. The Geometry of Linear Equations
2. Elimination and Matrix Operations (elimination, pivots, etcetera, different viewpoints of AB and Ax and x^TA,
e.g. as linear combinations of rows or columns)
3. Elimination Matrices and Matrix Inverses (row operations = multiplying on left by elimination matrices, Gauss-
Jordan elimination and what happens when you repeat the elimination steps on I)
4. A = LU Factorization (for example, the relationship between L and the elimination steps, and solving problems
with A in terms of the triangular matrices L and U)
5. Permutations, Dot Products, and Transposes (relationship between dot products and transposes, (AB)^T = B^TA^T ,
permutation matrices, etcetera)
6. Vector Spaces and Subspaces (for example, the column space and nullspace, what is and isn’t a subspace in
general, and other vector spaces/subspaces e.g. using matrices and functions)
7. Solving Ax = 0 (the nullspace), echelon form U, row-reduced echelon form R (rank, free variables, pivot variables,
special solutions, etcetera)
8. Solving Ax = 0 for nonsquare A (particular solutions, relationship of rank/nullspace/columnspace to existence
and uniqueness of solutions)

If there is one central technique in all of these lectures, it is elimination. You should know elimination forwards and
backwards. Literally: we might give you the final steps and ask you to work backwards, or ask you what properties
of A you can infer from certain results in elimination. Know how elimination relates to nullspaces and column spaces:
elimination doesn’t change the nullspace, which is why we can solve Rx = 0 to get the nullspace, while it does change
the column space...but you can check that b is in the column space of A by elimination (if elimination produces a zero
row from A, the same steps should produce a zero row from b if b is in the column space). Understand why elimination
works, not just how. Know how/why elimination corresponds to matrix operations (elimination matrices and L).

One common mistake that I’ve warned you about before is: never compute the inverse of a matrix, unless you are
specifically asked to. If you find yourself calculating A^-1 in order to compute x = A^-1b, you should instead solve
Ax = b for x by elimination & backsubstitution. Computing the inverse matrix explicitly is a lot more work, and more
error prone...and fails completely if A is singular or nonsquare.

Some practice problems

The 18.06 web site has exams from previous terms that you can download, with solutions. I’ve listed a few practice
exam problems that I like below, but there are plenty more to choose from. Note, however that there will be no
questions asking explicitly about linear independence, basis, dimension, or the row space or left nullspace. Reviewing
the homework and solutions is always a good idea, too. The exam will consist of 3 or 4 questions (perhaps with several
parts each), and you will have one hour.

1. A is a 4*4 matrix with rank 2, and Ax = b for some b has three solutions

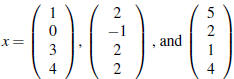
Give the nullspace N(A).

2. If we do a sequence of column operations (adding multiples of one column to another column) on a square
matrix A and obtain the identity matrix I, then what do we get if we do the same sequence of column operations
on A^-1? (Express your answer in terms of A and/or A^-1.)

3. If A is 5*3, B is 4*5, and C(A) = N(B), then what is BA?

4. If A and B are matrices of the same size andC(A)=C(B), doesC(A+B)=C(A)? If not, give a counter-example.

5. (From spring 2007, exam 1 problem 1.) Are the following sets of vectors in R³ subspaces? Explain your
answers.

(a) vectors (x,y, z)^T such that 2x-2y+z = 0
(b) vectors (x,y, z)^T such that x^2-y^2+z = 0
(c) vectors (x,y, z)^T such that 2x-2y+z = 1
(d) vectors (x,y, z)^T such that x = y and x = 2z
(e) vectors (x,y, z)^T such that x = y or x = 2z

6. (From spring 2007, exam 1 problem 3.) Consider the matrix

(a) What is the rank of A?
(b) Find a matrix B such that the column space C(A) of A equals the nullspace N(B) of B.

(c) Which of the following vectors belong to the column spaceC(A)?

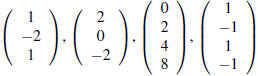
7. (From spring 2007, exam 1 problem 4.) Consider the matrix

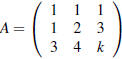
(a) For which values of k will the system 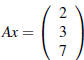have a unique solution?

(b) For which values of k will the system from (a) have an infinite number of solutions?
(c) For k = 4, find the LU decomposition of A.

(d) For all values of k, find the complete solution to 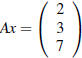. (You might have to consider several cases.)

8. (From fall 2006 exam 1, problem 4.)

(a) If A is a 3-by-5 matrix, what information do you have about the nullspace of A?
(b) In the vector space M of all 3*3 matrices, what subspace is spanned by all possible row-reduced echelon
forms R?

9. (From spring 2006 exam 1, problem 3.) [Hint: best if you don’t work too hard on this problem!] Let

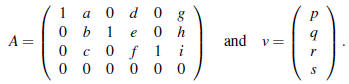
(a) Find the complete solution to Ax = v if s = 1.
(b) Find the complete solution to Ax = v if s = 0.

10. (From spring 2005 exam 1, problem 1.) Suppose A is reduced by the usual row operations to

Find the complete solution (if any exists) to this system involving the original A:

Ax = sum of the columns of A:

11. (From spring 2005 exam 1, problem 2.) Suppose the 4*4 matrices A and B have the same column space. They
may not have the same columns!

(a) Are they certain to have the same number of pivots? YES or NO. Explain.
(b) Are they certain to have the same nullspace? YES or NO. Explain.
(c) If A is invertible, are you sure that B is invertible? YES or NO. Explain.

12. (From spring 2005 exam 1, problem 3.)

(a) Reduce A to an upper-triangular matrix U and carry out the same elimination steps on the right side b:

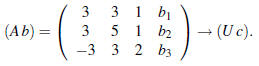
Factor the 3*3 matrix A into LU (lower triangular times upper triangular).

(b) If you change the last (lower-right) entry in A from 2 to _____ to get a new matrix A_new, then A_new
becomes singular. Fill in the blank, and describe its column space exactly.

(c) In that singular case from (b), what conditions on b₁, b₂, and b₃ allow A_newx = b to be solved?

(d) Write down the complete solution to 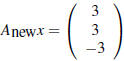(the first column of A_new).

Solutions

The solutions for all problems from previous exams are posted on the 18.06 web page. Solutions to the first four
problems are:

1. The differences 0 between the solutions must be in the nullspace. We have three solutions, hence two differences:

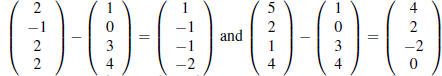The rank of A is 2 and it has 4 columns,

so we only need two independent nullspace vectors to span the nullspace. Hence the nullspace is the span of
these two difference vectors (which clearly aren’t multiples of one another).

2. A sequence of column operations corresponds to multiplying A on the right by some matrix E, like in the
problem sets. But if AE = I, then E must be A^-1. Doing the same operations on A^-1 gives A^-1E = A^-1A^-1 =
A^-2.

3. BA is a 4*3 matrix. Since C(A) = N(B), then BAx for any x gives B multiplied by something in N(B), which
gives zero. Since BAx = 0 for any x, we must have

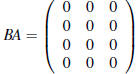
4. No. A simple example is B = -A for any nonzero A. C(-A) =C(A) (it’s the same columns, just multiplied by
-1), but A+(-A) = 0 and the column space of the zero matrix is just .
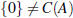