Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

College Algebra Study Guide

E.12

47. Solve the inequality x² - x > 12.
Answer: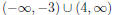

48. Solve the inequality x³ - x² ≤ 6x.
Answer: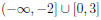

49. Solve the inequality .
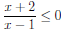Answer: [-2, 1)
50. Solve the inequality and write your answer in interval notation,
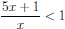
Answer: (-1/4, 0)

51. A Web-based embroidery company makes monogrammed napkins. The pro t associated with
producing x orders of napkins is governed by the equation

P(x) = -x² + 130x - 3000

Determine how many orders the company should accept to make a pro t.
Answer: 31 to 99 orders will yield a pro t. (i.e. (30, 100)).

E.13
52. State the order of the matrix 2

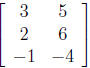
Answer: 3 x 2, (i.e 3 rows by 2 columns )

53. Solve for the indicated variables.

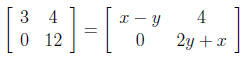
Answer: x = 6, y = 3
54. Let 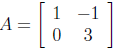and 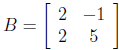. Find 2A - 3B and BA.
Answer: 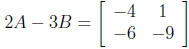, and .

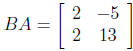55. The IRS allows and individual to deduct business expenses in the following way: $0.45 per
mile driven, 50% of entertainment cost, and 100% of actual expenses. Represent these deductions as
a row matrix A. In 2006, Joe had the following business expenses: $2, 700 in entertainment, $15, 200
actual expenses, and he drove 7523 miles. Represent Joe's expenses as a column matrix B. Multiply
these matrices (AB) to find the total amount of business expenses Joe can claim on his 2006 tax form.

Answer: .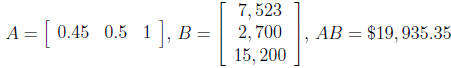

56. Find the inverse (if it exists) of the matrix
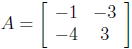
Answer: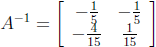

E.14

57. Find the fifth term in the expansion of (s - 3y)⁷.
Answer: The fifth term is 2835s³y⁴.

58. Apply the binomial theorem to expand (2z - 3y)⁴:
Answer: (2z - 3y)⁴ = 16z⁴ - 96z³y + 216z²y² - 216zy³ + 81y⁴

E.15

59. The 54th and 4th term of an arithmetic sequence are -61 and 64, respectively. Find the 23rd
term in the sequence.
Answer: the 23rd term is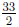

60. Find the sum of the first 11 terms of the Arithmetic sequence 9, 17, 25, 33, ...
Answer: 539.

61. Find the first four terms and the 10th term of the sequence given by .
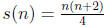Answer: .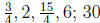

62. Give the first four terms of the geometric sequence for which 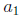= -5 and r = 4:
Answer: -5,-20,-80,-320

63. Find the next three terms of the geometric sequence 27,-9, 3,-1, ...
Answer: .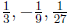

64. For the sequence . write a formula for the general term an:
Answer: or .

65. Find the infinite sum 0.5 + 0.05 + 0.005 +... .
Answer: .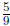

66. Find the sum of the first seven terms of the sequence
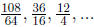
Answer: .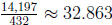

E.16

67. Use Cramer's Rule to solve for x and y.

3x - 4y = 1
4x - 2y = 8

Answer: x = 3 and y = 2

68. Solve the system of equations by substitution or addition method:

x + y + z = 0
2x + z = -1
x - y - z = 2

Answer: x = 1, y = 2, z = -3

69. Solve the system by the method of your choice:

2u + 5v = 7
3u - v = 5

Answer: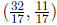

70. A Honda Accord gets approximately 26 mpg on the highway and 19 mpg in the city. You drove
349.5 miles on a full 16 gallon tank. Assuming you drove on both highway and city, approximately
how many miles did you drive in the city and how many on the highway?

Answer: 169 miles on the highway, 180.5 miles in the city .

71. Find the determinant

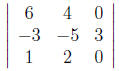
Answer: -24

E. 17

72. Prove by mathematical induction that, for all positive integers n,

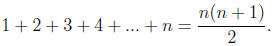
Solution:
STEP 1. First we show that the formula above holds true when n = 1, i.e.

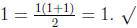
STEP 2. Now we assume that the formula above holds true for any k < n, that is

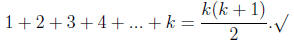
STEP 3. If we can show that the formula above holds for k + 1 term, we are done. So, adding
k + 1 to both sides in step 2 we get,

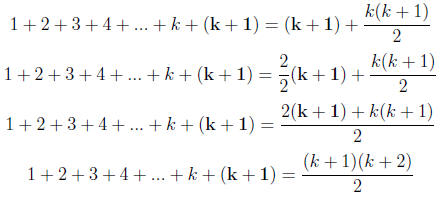
note that the right hand side is the value 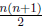when (k + 1) is substituted for n.
Hence if the formula is true for k, we have proved it is also true for k + 1, but since k is any
positive integer the formula is true for ALL positive integers n.
...Please see your instructor or tutor for a more detailed reasoning.

Extras:

73. Find the center and radius given the following equation of a circle:

x² + y² + 6x + 2y + 6 = 0

Answer: Center: (-3,-1) radius: r = 2

74. Use the Remainder Theorem to find P(-5) if P(x) = x⁶ + 6x⁵ + 5x³ - 6x² - 24
Answer: P(-5) = -3924

75. Find the sum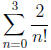
Answer: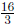

*NOTE: The problems in this document are a selection of problems from many sources, including College Algebra textbooks, Mymathlab,
Wileyplus and East field College math faculty. This document should give you an idea of the topics you need know after completing College
Algebra, this document does not intend to give information on any type of examination, including the final exam.

Home