Math Homework Solutions

1. Graph the following functions. Show all your work!

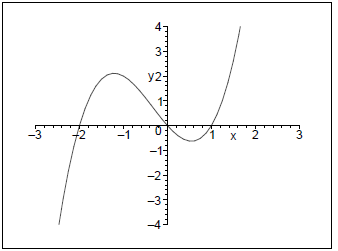
(a) f(x) = x(x − 1)(x + 2)
Solution:
End behavior:
As x → ∞ f(x) → (+)(+)(+) = +∞
As x → −∞ f(x) → (−)(−)(−) = −∞
y-intercept: 0
x-intercepts: 0, 1, −2 (all multiplicity 1)
Hence the graph is

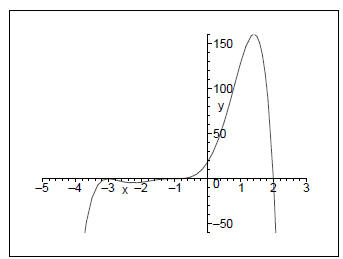
(b) f(x) = (x + 3)²(2 − x)(x + 1)³
Solution:
End behavior:
As x → ∞ f(x) → (+)²(−)(+)³ = −∞
As x → −∞ f(x) → (−)²(+)(−)³ = −∞
y-intercept: 18
x-intercepts: −3 (multiplicity 2), 2 (multiplicity 1), −1 (multiplicity
3)

Hence the graph is

2. Find the quotient and remainder for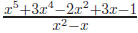
Solution:

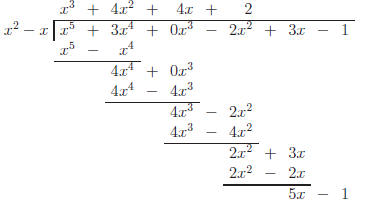
Hence the quotient is x³ + 4x² + 4x + 2 with a remainder of 5x − 1.

3. Find f(−5) if f(x) = x⁵ + 8x⁴ + 12x³ − 14x² − 22
Solution:
Use the remainder theorem and synthetic division:

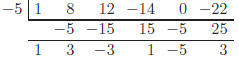
Hence f(−5) = 3

4. Find all zeros of the function. Show all your work!

(a) f(x) = x³ − 4x² − 3x + 18
Solution:
List the possible rational zeros: ±1,±2,±3,±6,±9,±18
Clearly 1 and −1 are not zeros, so we try 2:

Not a zero, so we try −2:

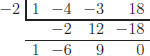
This is a zero, so we can factor the polynomial as (x+2)(x−6x+9)
We can now factor the quadratic term to get: (x + 2)(x − 3)²
Hence the zeros are −2 and 3 (multiplicity 2).

(b) f(x) = x⁴ − 2x³ − 7x² + 20x − 12
Solution:
First list the possible rational zeros: ±1,±2,±3,±4,±6,±12
First check 1:

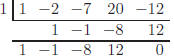
Hence we can factor the polynomial as (x − 1)(x³ − x² − 8x + 12)

We have to find another zero, the possible rational zeros remain the
same. It is easy to see that neither 1 or −1 is a zero, so we try 2:

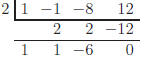
Hence 2 is a zero and we can factor the polynomial as (x − 1)(x −
2)(x² + x − 6)
Factoring the quadratic term we get (x − 1)(x − 2)(x − 2)(x + 3)
Hence the zeros are 1, 2 (multiplicity 2), −3

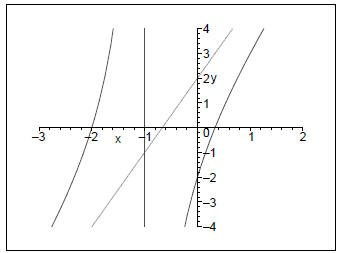
5. Graph the function 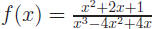. Explain all your steps!
Solution:
First factor the polynomials: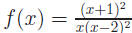
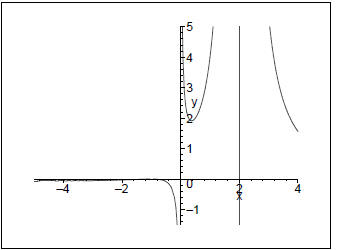
Horizontal asymptote: y = 0 (degree smaller in numerator)
Vertical asymptotes: 0 (multiplicity 1), 2 (multiplicity 2)
y-intercept: none
x-intercept: −1 (multiplicity 2)
Steps to graph it: (from right to left)
First check the sign to the right off the vertical asymptote at x = 2.
It is positive, so the graph will be above the x- axis.
Thus it will go up on the right of the vertical asymptote at x = 2.
The vertical asymptote at x = 2 has multiplicity 2, so there will not be
a change in sign. Thus it is also going up to the left of the asymptote.
Now there is the vertical asymptote at x = 0. Since there is no x-
intercept between the two asymptotes, it will have to go up to the right
of this asymptote.
This asymptote has multiplicity 1, so there is a sign change. Thus to
the left of the asymptote at x = 0 it will go down.
Now there is the x-intercept at −1. It has multiplicity 2, so there will
not be a sign change. Hence to the left of this intercept it will also be
negative.

Thus the graph is:

6. Find the slant asymptote of 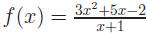and graph the function.
Solution:
First find the slant asymptote by synthetic division:

Hence the function is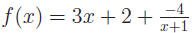
Thus the slant asymptote is y = 3x + 2
Factor the numerator: 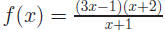Vertical asymptote: x = −1
y-intercept: −2
x-intercepts: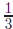 , −2

Then the graph is